Bonjour,
Je souhaiterais résoudre une équation sur le calcul du taux actuariel d'un emprunt obligataire. Peut importe ce point. Une fois l'équation posé, ca sera plus clair pour vous :
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
Comment puis-je résoudre cette équation ? Il faut utiliser les ln mais je ne me souviens plus du tout...
Merci beaucoup pour votre aide.
Cordialement.
Nicolas.
Résolution d'équation avec puissance.
16 messages
- Page 1 sur 1
par siger » 01 Juin 2015, 15:39
bonjour
avec a= 1/(1+i ) on peut ecrire
99= 10*( a + a^2 + a^3 + a^4 +a^5)
mais .... quelle equation? ou est la variable?
.....
avec a= 1/(1+i ) on peut ecrire
99= 10*( a + a^2 + a^3 + a^4 +a^5)
mais .... quelle equation? ou est la variable?
.....
par nikholas » 01 Juin 2015, 16:00
Bonjour Siger.
La variable est i. Il me faut trouver le taux fixe i. Et je ne sais pas trop comment gérer les puissances dans cette équation...
Est-ce plus clair ?
Merci pour votre réponse
La variable est i. Il me faut trouver le taux fixe i. Et je ne sais pas trop comment gérer les puissances dans cette équation...
Est-ce plus clair ?
Merci pour votre réponse
par SAGE63 » 01 Juin 2015, 16:38
nikholas a écrit:Bonjour Siger.
La variable est i. Il me faut trouver le taux fixe i. Et je ne sais pas trop comment gérer les puissances dans cette équation...
Est-ce plus clair ?
Merci pour votre réponse
bonjour
C'est une équation pour déterminer une VAN ou un TRI.
Pour calculer "i", je suppose le taux annuel, il existe plusieurs méthodes :
a) l'utilisation de calculatrice perfectionnée
b) l'utilisation de solveur des tableurs
c) la méthode des approches successives : on prend
*1- le taux i = 5 % et on voit le résultat
*2- le taux i = 10 % et on voit le résultat
*3 etc pour approcher du taux le plus juste
Dites moi le taux que vous trouvez.
Bons calculs
par WillyCagnes » 01 Juin 2015, 17:31
bsr
pour ton équation si tu es sûr du 1100/(1+i);) ?
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
je trouve i=0,76414
pour ton équation si tu es sûr du 1100/(1+i);) ?
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
je trouve i=0,76414
par WillyCagnes » 01 Juin 2015, 17:36
bsr
si tu es sûr de 1100/(1+i);) ?
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
je trouve i=0,102655
si tu es sûr de 1100/(1+i);) ?
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
je trouve i=0,102655
par nikholas » 16 Juin 2015, 11:02
Bonjour,
Désolé je n'avais pas recu de notification comme quoi j'avais recu une réponse.
Oui en faite c'est le TRI. Mais j'aimerais connaitre une autre méthode que l'extrapolation linéaire.
J'aurais aimé résoudre cette équation de cette manière :
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
990= 100*(1+i)^-1 + 100*(1+i)^-2 + 100*(1+i)^-3 + 100*(1+i)^-4 + 1100*(1+i)^-5
990=100*(-ln(1+i)) + 100*(-2ln(1+i)) + 100*(-3ln(1+i)) + 100*(-4ln(1+i)) +1100*(-5ln(1+i))
Et après pouvoir résoudre l'équation de ln avec exponentiel pour que finalement on obtienne quelque chose de cette forme :
ln(1+i)=990
Je ne sais pas si je suis clair?
Désolé je n'avais pas recu de notification comme quoi j'avais recu une réponse.
Oui en faite c'est le TRI. Mais j'aimerais connaitre une autre méthode que l'extrapolation linéaire.
J'aurais aimé résoudre cette équation de cette manière :
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
990= 100*(1+i)^-1 + 100*(1+i)^-2 + 100*(1+i)^-3 + 100*(1+i)^-4 + 1100*(1+i)^-5
990=100*(-ln(1+i)) + 100*(-2ln(1+i)) + 100*(-3ln(1+i)) + 100*(-4ln(1+i)) +1100*(-5ln(1+i))
Et après pouvoir résoudre l'équation de ln avec exponentiel pour que finalement on obtienne quelque chose de cette forme :
ln(1+i)=990
Je ne sais pas si je suis clair?
par SAGE63 » 16 Juin 2015, 11:15
[quote="nikholas"]Bonjour,
Désolé je n'avais pas recu de notification comme quoi j'avais recu une réponse.
Oui en faite c'est le TRI. Mais j'aimerais connaitre une autre méthode que l'extrapolation linéaire.
J'aurais aimé résoudre cette équation de cette manière :
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
990= 100*(1+i)^-1 + 100*(1+i)^-2 + 100*(1+i)^-3 + 100*(1+i)^-4 + 1100*(1+i)^-5
990=100*(-ln(1+i)) + 100*(-2ln(1+i)) + 100*(-3ln(1+i)) + 100*(-4ln(1+i)) +1100*(-5ln(1+i))
Et après pouvoir résoudre l'équation de ln avec exponentiel pour que finalement on obtienne quelque chose de cette forme :
ln(1+i)=990
Bonjour
Pour calculer "i" le taux d'intérêt dans cette équation, à ma connaissance, la seule méthode qui existe quand "n" est "important", est la méthode d'approche par essais successifs.
Moi aussi je suis preneur d'une solution algébrique quand "n" est égal à 5, 6 et plus.
Désolé je n'avais pas recu de notification comme quoi j'avais recu une réponse.
Oui en faite c'est le TRI. Mais j'aimerais connaitre une autre méthode que l'extrapolation linéaire.
J'aurais aimé résoudre cette équation de cette manière :
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
990= 100*(1+i)^-1 + 100*(1+i)^-2 + 100*(1+i)^-3 + 100*(1+i)^-4 + 1100*(1+i)^-5
990=100*(-ln(1+i)) + 100*(-2ln(1+i)) + 100*(-3ln(1+i)) + 100*(-4ln(1+i)) +1100*(-5ln(1+i))
Et après pouvoir résoudre l'équation de ln avec exponentiel pour que finalement on obtienne quelque chose de cette forme :
ln(1+i)=990
Bonjour
Pour calculer "i" le taux d'intérêt dans cette équation, à ma connaissance, la seule méthode qui existe quand "n" est "important", est la méthode d'approche par essais successifs.
Moi aussi je suis preneur d'une solution algébrique quand "n" est égal à 5, 6 et plus.
par nikholas » 16 Juin 2015, 11:24
SAGE63 a écrit:nikholas a écrit:Bonjour,
Désolé je n'avais pas recu de notification comme quoi j'avais recu une réponse.
Oui en faite c'est le TRI. Mais j'aimerais connaitre une autre méthode que l'extrapolation linéaire.
J'aurais aimé résoudre cette équation de cette manière :
990 = 100/(1+i)¹ + 100/(1+i)² + 100/(1+i)³ + 100/(1+i);) + 1100/(1+i);)
990= 100*(1+i)^-1 + 100*(1+i)^-2 + 100*(1+i)^-3 + 100*(1+i)^-4 + 1100*(1+i)^-5
990=100*(-ln(1+i)) + 100*(-2ln(1+i)) + 100*(-3ln(1+i)) + 100*(-4ln(1+i)) +1100*(-5ln(1+i))
Et après pouvoir résoudre l'équation de ln avec exponentiel pour que finalement on obtienne quelque chose de cette forme :
ln(1+i)=990
Bonjour
Pour calculer "i" le taux d'intérêt dans cette équation, à ma connaissance, la seule méthode qui existe quand "n" est "important", est la méthode d'approche par essais successifs.
Moi aussi je suis preneur d'une solution algébrique quand "n" est égal à 5, 6 et plus.
D'accord, merci beaucoup pour votre réponse. J'aurais du faire maths sup pour apprendre cette méthode sans doute^^.
Bonne journeé.
par Ben314 » 16 Juin 2015, 14:39
Salut,
La méthode "proposée" par nikholas, c'est "du grand n'importe quoi" : lorsque l'on apprend ce qu'est la fonction log, l'une des première chose qu'on voit, cest que log(a*b)=log(a)log(b) mais qu'on ne peut pas simplifier log(a+b) [en tout cas, ça ne risque pas d'être égal à log(a)+log(b) !!!]
Sinon, si on veut aller un peu plus vite que par bête "d'approche par essais successifs", la méthode des tangentes marche très bien dans ce cas là et donne une très bonne approximation en peu d'itérations.
La méthode "proposée" par nikholas, c'est "du grand n'importe quoi" : lorsque l'on apprend ce qu'est la fonction log, l'une des première chose qu'on voit, cest que log(a*b)=log(a)log(b) mais qu'on ne peut pas simplifier log(a+b) [en tout cas, ça ne risque pas d'être égal à log(a)+log(b) !!!]
Sinon, si on veut aller un peu plus vite que par bête "d'approche par essais successifs", la méthode des tangentes marche très bien dans ce cas là et donne une très bonne approximation en peu d'itérations.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par zygomatique » 16 Juin 2015, 16:13
salut
 + 100/(1+i)^2 + 100/(1+i)^3 + 100/(1+i)^4 + 100/(1+i)^5 9,9(1 + i)^5 = \dfrac {1 - (1 + i)^{-5}}{1 - \dfrac 1{1 + i}} 9,9i(1 + i)^4 = 1 - (1 + i)^{-5})
si i < 1 une bonne approximation de i est la solution positive de l'équation = 5i)
.... si elle existe ....
si i < 1 une bonne approximation de i est la solution positive de l'équation
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par Ben314 » 16 Juin 2015, 19:36
L'équation ^2}+\frac{S}{(1+i)^3}+\cdots +\frac{S}{(1+i)^N}=T\ (#))
équivaut à ^{-N}}{1-(1+i)^{-1}}=\frac{T}{S})
soit encore =\frac{T}{S}\)
où =\frac{1-(1+i)^{-N}}{i}\)
(et =N)
).
La méthode de Newton consiste a partir d'un i "proche" de l'unique solution de)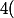
puis à itérer la fonction =i-\frac{f(i)-\frac{T}{S}}{f'(i)}=\frac{ (1+i)+Ni\big( \frac{T}{S} i-1)-(1+i)^{1-N} } { \frac{T}{S}(1+i)+N\big(\frac{T}{S}i-1\big)})
Comme pour i proche de 0 on a\simeq N-\frac{N(N+1)}{2}i\)
on peut commencer les itérations en partant de }{N(N+1)})
.
Par exemple, si N=5 , T=990 , S=100 en utilisant un tableur, on a :
i0 = -0,326666666
i1 = -0,240205289
i2 = -0,198541271
i3 = -0,191791718
i4 = -0,191646676
i5 = -0,191646611
On pourrait aller un plus vite en utilisant le D.L. de f au voisinage de 0 à l'ordre 2 pour déterminer i0, mais je pense que même comme ça, ça donne la valeur de i en quelques itérations.
La méthode de Newton consiste a partir d'un i "proche" de l'unique solution de
Comme pour i proche de 0 on a
Par exemple, si N=5 , T=990 , S=100 en utilisant un tableur, on a :
i0 = -0,326666666
i1 = -0,240205289
i2 = -0,198541271
i3 = -0,191791718
i4 = -0,191646676
i5 = -0,191646611
On pourrait aller un plus vite en utilisant le D.L. de f au voisinage de 0 à l'ordre 2 pour déterminer i0, mais je pense que même comme ça, ça donne la valeur de i en quelques itérations.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par SAGE63 » 16 Juin 2015, 20:04
Ben314 a écrit:L'équation
La méthode de Newton consiste a partir d'un i "proche" de l'unique solution de
Comme pour i proche de 0 on a
Par exemple, si N=5 , T=990 , S=100 en utilisant un tableur, on a :
i0 = -0,326666666
i1 = -0,240205289
i2 = -0,198541271
i3 = -0,191791718
i4 = -0,191646676
i5 = -0,191646611
On pourrait aller un plus vite en utilisant le D.L. de f au voisinage de 0 à l'ordre 2 pour déterminer i0, mais je pense que même comme ça, ça donne la valeur de i en quelques itérations.
Bonsoir
UNE PRECISION :
NIKLOLAS avait donné comme équation :
990 = [100/(1+i)¹ ] + [100/(1+i)² ] + [100/(1+i)³ ] + [100/(1+i);) ] + [1100/(1+i);) ]
Dernier terme différent des autres
par Ben314 » 17 Juin 2015, 03:04
Effectivement, j'avais pas fait gaffe...SAGE63 a écrit:Bonsoir
UNE PRECISION :
NIKLOLAS avait donné comme équation :
990 = [100/(1+i)¹ ] + [100/(1+i)² ] + [100/(1+i)³ ] + [100/(1+i);) ] + [1100/(1+i);) ]
Dernier terme différent des autres
ça rend les formules un peu plus compliquées, mais le principe est exactement le même :
La fonction a itérer est alors
Et, comme au voisinage de 0, on a
Avec N=5 ; S=100 ; R=1100 ; T=990 le tableur donne
i0 = 0,078
i1 = 0,1012
i2 = 0,1026505
i3 = 0,10265589704
i4 = 0,102655897116246
Donc en deux itérations de la fonction
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par zygomatique » 17 Juin 2015, 16:59
SAGE63 a écrit:Bonsoir
UNE PRECISION :
NIKLOLAS avait donné comme équation :
990 = [100/(1+i)¹ ] + [100/(1+i)² ] + [100/(1+i)³ ] + [100/(1+i);) ] + [1100/(1+i);) ]
Dernier terme différent des autres
certes oui ... mais probablement une erreur de double frappe ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
par SAGE63 » 17 Juin 2015, 17:08
zygomatique a écrit:certes oui ... mais probablement une erreur de double frappe ...
Bonjour
Peut être pas :
Enoncé possible :
Vous avez souscrit à une obligation pour un montant nominal de 1 000 euros payée 990 euros.
Cette obligation rapporte 10 % du nominal l'an.
Cette obligation est remboursée au bout de 5 ans à la valeur nominale.
Quel est le taux de rendement au bout de 5 ans ?
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :