Bonjour à tous,
J'aurais besoin de votre aide pour résoudre cette démonstration matricielle:
Montrez que toute matrice carrée A peut sexprimer dune façon unique comme la somme dune matrice symétrique et dune matrice antisymétrique.
Merci beaucoup à l'avance :we:
Pandableu
Démonstration matricielle
4 messages
- Page 1 sur 1
pour stimuler l'imagination:
=\frac{e^{x}+e^{-x}}{2})
=\frac{e^{x}-e^{-x}}{2})
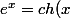+sh(x))
une fonction est somme d'une fonction paire et d'une fonction impaire,et ce,
de façon unique.
=\frac{1}{2} (f(x)+f(-x))+\frac{1}{2} (f(x)-f(-x)))
Pour une matrice, à quoi peut on penser ?
mode on
A=1/2 (A+tA)+1/2 (A-tA) où tA est la matrice transposée de A
mode off
si l'on ne pense à rien, poser A=M+N où M est symétrique et N antisymétrique et
calculer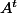
une fonction est somme d'une fonction paire et d'une fonction impaire,et ce,
de façon unique.
Pour une matrice, à quoi peut on penser ?
mode on
A=1/2 (A+tA)+1/2 (A-tA) où tA est la matrice transposée de A
mode off
si l'on ne pense à rien, poser A=M+N où M est symétrique et N antisymétrique et
calculer
Il faut surtout miser sur le côté unique de la matrice
Montrez que toute matrice carrée A peut sexprimer dune façon unique comme la somme dune matrice symétrique et dune matrice antisymétrique.
Soit deux matrices carrées:
Symétrique;)(A+A^T )
Antisymétrique;)(A-A^T)
Je n'ai pas vraiment compris ta réponse... :triste:
Soit deux matrices carrées:
Symétrique;)(A+A^T )
Antisymétrique;)(A-A^T)
Je n'ai pas vraiment compris ta réponse... :triste:
mathelot a écrit:pour stimuler l'imagination:
une fonction est somme d'une fonction paire et d'une fonction impaire,et ce,
de façon unique.
Pour une matrice, à quoi peut on penser ?
mode on
A=1/2 (A+tA)+1/2 (A-tA) où tA est la matrice transposée de A
mode off
si l'on ne pense à rien, poser A=M+N où M est symétrique et N antisymétrique et
calculer
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
