DM produits scalaires
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Matheuseendiff
- Membre Naturel
- Messages: 17
- Enregistré le: 11 Déc 2013, 15:48
-
 par Matheuseendiff » 31 Mai 2015, 17:22
par Matheuseendiff » 31 Mai 2015, 17:22
Bonjour,Je n'y arrive pas :mur:,, j'ai du mal à le commencer , merci de votre aide !
Le voici :
Partie 1-Distance d'un point à une droite
On se place dans un repère orthonormé du plan. Soit (d) une droite d'équation ax+by+c=0 avec a et b différents de 0 de vecteur normal n(ab) et soit A(xa;ya) un point du plan. Enfin, soit H ( xh;yh) le projeté orthogonal de A sur la droite (d). On définit la distance du point A à la droite (d) comme étant la distance AH.
1) Justifier que les vecteurs n et AH sont colinéaires
2) En déduire que /n.AH/= valeur absolue du vecteur n * AH
3) Justifier que vecteur n.AH = -axA-byA-c
4) En déduire que d(A;D)= norme de axA+byA+c/racinecarré(a²+b²)
Partie 2 Applications
1)On donne les 3 points A(1;2),B(-3;-4) et C(6;1)
a) Démontrer qu'une équation cartésienne de la droite (AB) est donnée par : 3x-2y+1=0
b) Déterminer la distance du point C à la droite (AB)
c) En déduire l'aire du triangle ABC
merci de m'aider ,
-
mathelot
 par mathelot » 31 Mai 2015, 17:34
par mathelot » 31 Mai 2015, 17:34
pour la (1), les droites (AH) et
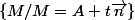
sont deux droites perpendiculaires à (d).
En dimension 2 , elles sont donc parallèles.
et leurs vecteurs directeurs
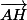
et
)
colinéaires
pour la (2)
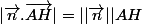
+b(y_H-y_A)|=\sqrt{a^2+b^2} AH)
|=\sqrt{a^2+b^2} AH) (1)
(1)(1) se simplifie car
)
-
Matheuseendiff
- Membre Naturel
- Messages: 17
- Enregistré le: 11 Déc 2013, 15:48
-
 par Matheuseendiff » 31 Mai 2015, 17:42
par Matheuseendiff » 31 Mai 2015, 17:42
mathelot a écrit:pour la (1), les droites (AH) et
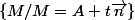
sont deux droites perpendiculaires à (d).
En dimension 2 , elles sont donc parallèles.
et leurs vecteurs directeurs
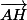
et
)
colinéaires
Comment ça t
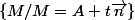
?
-
mathelot
 par mathelot » 31 Mai 2015, 18:00
par mathelot » 31 Mai 2015, 18:00
c'est la description de la droite perpendiculaire à (d) passant par A.
Un de ses vecteurs directeurs est
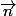
-
Matheuseendiff
- Membre Naturel
- Messages: 17
- Enregistré le: 11 Déc 2013, 15:48
-
 par Matheuseendiff » 31 Mai 2015, 18:38
par Matheuseendiff » 31 Mai 2015, 18:38
mathelot a écrit:c'est la description de la droite perpendiculaire à (d) passant par A.
Un de ses vecteurs directeurs est
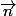
Pourriez-vous m'expliquer la question n3, aussi , cela serait gentil ,je seche :doh:
-
mathelot
 par mathelot » 31 Mai 2015, 19:52
par mathelot » 31 Mai 2015, 19:52
Matheuseendiff a écrit:Pourriez-vous m'expliquer la question n3, aussi , cela serait gentil ,je seche :doh:
en valeur absolue
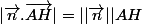

+b(y_H-y_A)=)
)
mais H est le projeté de A sur (d), il appartient à (d), donc
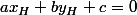
mézalor

)
d'où le calcul de AH (=d(A,(d)))
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 31 Mai 2015, 19:58
par titine » 31 Mai 2015, 19:58
vec(n) (a ; b)
vec(AH) (xH-xA ; yH-ya)
vec(n).vec(AH) = a(xH-xA) + b(yH-ya)
= axH - axA + byH - byA = -axA - byA + axH + byH
Mais comme H appartient à la droite d'équation ax + by + c = 0 alors axH + byH + c = 0
Donc axH + byH = -c
On a donc bien : vec(n).vec(AH) = -axA - bxA - c
-
mathelot
 par mathelot » 01 Juin 2015, 10:02
par mathelot » 01 Juin 2015, 10:02
Matheuseendiff a écrit:
4) En déduire que d(A;D)= norme de axA+byA+c/racinecarré(a²+b²)
c'est une valeur absolue.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
