Nombre dérivé
18 messages
- Page 1 sur 1
Fonction dérivé
Bonjour tout le monde,
J'ai un dm de math a faire et je bloque sur un exercice, pouvez vous m'aidez ?
Exercice :
Il est proposé dans cet exercice d'étudier f(x)=-x²+4x-3 sur l'intervalle [-1;5] et d'en tracer la courbe représentative.
a) Réaliser le tableau de variation de cette fonction.
b) Calculer le nombre dérivé f'(x) pour x=0, x=1, x=3, x=4. En déduire le coefficient directeur de la tangente à la courbe aux points x=0, x=1, x=3, x=4.
Je pense avoir réussi le petit a et la première partie du petit b mais je ne suis pas sur.
Merci d'avance pour votre aide.
J'ai un dm de math a faire et je bloque sur un exercice, pouvez vous m'aidez ?
Exercice :
Il est proposé dans cet exercice d'étudier f(x)=-x²+4x-3 sur l'intervalle [-1;5] et d'en tracer la courbe représentative.
a) Réaliser le tableau de variation de cette fonction.
b) Calculer le nombre dérivé f'(x) pour x=0, x=1, x=3, x=4. En déduire le coefficient directeur de la tangente à la courbe aux points x=0, x=1, x=3, x=4.
Je pense avoir réussi le petit a et la première partie du petit b mais je ne suis pas sur.
Merci d'avance pour votre aide.
D'accord donc pour le petit a j'ai tout d'abord fait la fonction dérivé et j'ai trouvé ceci
f'(x) : -2x+4
Puis j'ai chercher pour quelle valeur de x f'(x) est égale a 0 :
f'(x) = 0
-2x+4=0
-2x=-4
x=2
Donc j'ai pu faire mon tableau de valeur, et j'ai trouvé une fonction croissante.
Pour le petit b j'ai trouver pour les nombres dérivé :
f'(0)=4 f'(1)=2 f'(3)=-2 f'(4)=4
f'(x) : -2x+4
Puis j'ai chercher pour quelle valeur de x f'(x) est égale a 0 :
f'(x) = 0
-2x+4=0
-2x=-4
x=2
Donc j'ai pu faire mon tableau de valeur, et j'ai trouvé une fonction croissante.
Pour le petit b j'ai trouver pour les nombres dérivé :
f'(0)=4 f'(1)=2 f'(3)=-2 f'(4)=4
Ericovitchi a écrit:Et bien montre nous ce que tu as fait si tu n'es pas sûr ?
D'accord donc pour le petit a j'ai tout d'abord fait la fonction dérivé et j'ai trouvé ceci
f'(x) : -2x+4
Puis j'ai chercher pour quelle valeur de x f'(x) est égale a 0 :
f'(x) = 0
-2x+4=0
-2x=-4
x=2
Donc j'ai pu faire mon tableau de valeur, et j'ai trouvé une fonction croissante.
Pour le petit b j'ai trouver pour les nombres dérivé :
f'(0)=4 f'(1)=2 f'(3)=-2 f'(4)=4
Bonjour,
tu as trouvé f'(x) : -2x+4 qui s'annule pour x=2, ce qui est juste.
Par contre ta conclusion sur la croissance est inexacte.
En effet, il faut que tu cherches pour quelles valeurs de x ta dérivée est positive (dans ce cas, la fonction sera croissante) et pour quelles valeurs de x elle est négative (dans ce cas, la fonction sera décroissante).
Tu rentreras tout cela dans un tableau de variations (et non dans un tableau de valeurs)
tu as trouvé f'(x) : -2x+4 qui s'annule pour x=2, ce qui est juste.
Par contre ta conclusion sur la croissance est inexacte.
En effet, il faut que tu cherches pour quelles valeurs de x ta dérivée est positive (dans ce cas, la fonction sera croissante) et pour quelles valeurs de x elle est négative (dans ce cas, la fonction sera décroissante).
Tu rentreras tout cela dans un tableau de variations (et non dans un tableau de valeurs)
annick a écrit:Bonjour,
tu as trouvé f'(x) : -2x+4 qui s'annule pour x=2, ce qui est juste.
Par contre ta conclusion sur la croissance est inexacte.
En effet, il faut que tu cherches pour quelles valeurs de x ta dérivée est positive (dans ce cas, la fonction sera croissante) et pour quelles valeurs de x elle est négative (dans ce cas, la fonction sera décroissante).
Tu rentreras tout cela dans un tableau de variations (et non dans un tableau de valeurs)
Ah oui je me suis tromper, je voulais dire un tableau de variation
Bonjour Ornella14,
La formule de la tangente au point est donnée par :
est donnée par : 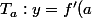(x-a)+f(a)) .
.
Il te reste plus ici qu'à remplacer par les points qui te sont demandés.
par les points qui te sont demandés.
Par exemple, pour , tu auras :
, tu auras :
(x-0)+f(0)=4x-3)
À noter que dans certains cas, le nombre dérivé s'obtient par la formule du taux d'accroissement :-f(a)}{x-a}) .
.
Mais, je ne pense pas que tu en aies besoin ici...
Voilà ! :ptdr:
La formule de la tangente au point
Il te reste plus ici qu'à remplacer
Par exemple, pour
À noter que dans certains cas, le nombre dérivé s'obtient par la formule du taux d'accroissement :
Mais, je ne pense pas que tu en aies besoin ici...
Voilà ! :ptdr:
Axiom a écrit:Bonjour Ornella14,
La formule de la tangente au pointest donnée par :
.
Il te reste plus ici qu'à remplacerpar les points qui te sont demandés.
Par exemple, pour, tu auras :
(x-0)+f(0)=4x-3)
À noter que dans certains cas, le nombre dérivé s'obtient par la formule du taux d'accroissement :.
Mais, je ne pense pas que tu en aies besoin ici...
Voilà ! :ptdr:
Bonjour, je n'ai pas tout compris car je n'est pas vu être formule dons mon cours mais merci beaucoup pour votre aide
C'est un double post : http://www.maths-forum.com/showthread.php?t=165631
C'est dommage car tu avais eu déjà pas mal d'aides et ici, tu demandes à tes interlocuteurs de tout recommencer (entre autres, cela aurait évité que l'on te demande si tu connaissais les dérivées, etc...)
Il vaut mieux que tu fasses remonter ton post plutôt que d'en ouvrir un autre qui te fait perdre ton temps et celui de ceux qui essayent de te répondre.
C'est dommage car tu avais eu déjà pas mal d'aides et ici, tu demandes à tes interlocuteurs de tout recommencer (entre autres, cela aurait évité que l'on te demande si tu connaissais les dérivées, etc...)
Il vaut mieux que tu fasses remonter ton post plutôt que d'en ouvrir un autre qui te fait perdre ton temps et celui de ceux qui essayent de te répondre.
18 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
