Exercice sur fonction - 2nde
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
popololita
- Membre Naturel
- Messages: 14
- Enregistré le: 18 Jan 2013, 17:17
-
 par popololita » 26 Mai 2015, 18:32
par popololita » 26 Mai 2015, 18:32
Soit f la fonction définie par : f(x) = 2x² + 4x-3 et g la fonction définie par : g(x) = -1/2x+4 (fraction donc 1 SUR 2).
1. montrer que pour tout x, f(x) peut s'écrire f(x) = 2(x+1)²-5
2. montrer que pour tout x, f(x) supérieur ou égal ) -5. Que peut-on déduire pour f.
3. Dresser le tableau de variations de la fonction f sur l'intervalle [-6;4].
4. résoudre algébriquement l'équation f(x) = 13.
Merci pour tout !!
-
Saiwen
- Membre Naturel
- Messages: 20
- Enregistré le: 26 Mai 2015, 19:48
-
 par Saiwen » 26 Mai 2015, 21:50
par Saiwen » 26 Mai 2015, 21:50
1)
Tu développes 2(x+1)²-5
= 2(x²+1+2x)-5
=2x²+2+4x-5
=2x²-3+4x
2)
f(x)>-5
2(x+1)²-5>-5
2(x+1)²>0
x+1=0
x=-1
le sommet de la fonction (qui est ici une parabole) est en x=-1 et y=-5
3)
Tableau, un peu la flemme
4)
f(13)=2*13²+4*13-3
=2*169+52-3
=387
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 26 Mai 2015, 22:41
par Pisigma » 26 Mai 2015, 22:41
popololita a écrit:Soit f la fonction définie par : f(x) = 2x² + 4x-3 et g la fonction définie par : g(x) = -1/2x+4 (fraction donc 1 SUR 2).
1. montrer que pour tout x, f(x) peut s'écrire f(x) = 2(x+1)²-5
2. montrer que pour tout x, f(x) supérieur ou égal ) -5. Que peut-on déduire pour f.
3. Dresser le tableau de variations de la fonction f sur l'intervalle [-6;4].
4. résoudre algébriquement l'équation f(x) = 13.
Merci pour tout !!
Bonsoir,
1. il faut écrire f(x)=2x²+4x-3 sous forme canonique
2. 2(x+1)² > 0 d'où...
4. on demande de résoudre 2x²+4x-3=13
-
popololita
- Membre Naturel
- Messages: 14
- Enregistré le: 18 Jan 2013, 17:17
-
 par popololita » 27 Mai 2015, 14:40
par popololita » 27 Mai 2015, 14:40
Pisigma a écrit:Bonsoir,
1. il faut écrire f(x)=2x²+4x-3 sous forme canonique
2. 2(x+1)² > 0 d'où...
4. on demande de résoudre 2x²+4x-3=13
ça ne m'aide pas, tu me dis juste les consignes..
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 27 Mai 2015, 14:49
par Pisigma » 27 Mai 2015, 14:49
popololita a écrit:ça ne m'aide pas, tu me dis juste les consignes..
1. f(x) doit s'écrire sous la forme
=a(x-\alpha)^2+\beta)
2. un carré est toujours ?
4. cela revient à résoudre 2x²+4x-3-13=0 soit 2x²+4x-16=0
-
popololita
- Membre Naturel
- Messages: 14
- Enregistré le: 18 Jan 2013, 17:17
-
 par popololita » 27 Mai 2015, 15:06
par popololita » 27 Mai 2015, 15:06
Pisigma a écrit:1. f(x) doit s'écrire sous la forme
=a(x-\alpha)^2+\beta)
2. un carré est toujours ?
4. cela revient à résoudre 2x²+4x-3-13=0 soit 2x²+4x-16=0
oui mais pour le 1. je fais comment alors ? je bloque vraiment..
et pour le 4. faut pas plutôt remplacer les x de la fonction par 13?
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 27 Mai 2015, 15:30
par Pisigma » 27 Mai 2015, 15:30
popololita a écrit:oui mais pour le 1. je fais comment alors ? je bloque vraiment..
et pour le 4. faut pas plutôt remplacer les x de la fonction par 13?
1.
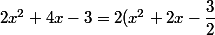=2[(x+1)^2-1-\dfrac{3}{2}]=2(x+1)^2-5)
4. on te demande de résoudre l'équation c'est à dire trouver les valeurs de x.
Tu peux factoriser ou utiliser le calcul du discriminant pour trouver x1 et x2
-
Saiwen
- Membre Naturel
- Messages: 20
- Enregistré le: 26 Mai 2015, 19:48
-
 par Saiwen » 27 Mai 2015, 19:47
par Saiwen » 27 Mai 2015, 19:47
Je t'ai donner toutes les réponses plus haut, tu n'as pas vu ?
-
Saiwen
- Membre Naturel
- Messages: 20
- Enregistré le: 26 Mai 2015, 19:48
-
 par Saiwen » 27 Mai 2015, 19:50
par Saiwen » 27 Mai 2015, 19:50
Pisigma a écrit:1.
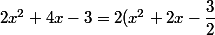=2[(x+1)^2-1-\dfrac{3}{2}]=2(x+1)^2-5)
4. on te demande de résoudre l'équation c'est à dire trouver les valeurs de x.
Tu peux factoriser ou utiliser le calcul du discriminant pour trouver x1 et x2
Je suis pas d'accord, si tu calcule x1 et x2 avec (-b-(+)

delta)/2a
Tu vas trouver les points X ou la parabole coupe l'axe des abcisses, et non pas f(x)=13
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 27 Mai 2015, 20:33
par Pisigma » 27 Mai 2015, 20:33
Saiwen a écrit:Je suis pas d'accord, si tu calcule x1 et x2 avec (-b-(+)

delta)/2a
Tu vas trouver les points X ou la parabole coupe l'axe des abcisses, et non pas f(x)=13
Les racines de 2x²+4x-16 remplacées dans 2x²+4x-3 donnent bien f(x)=13.
Ecrire f(13) signifie remplacer x par 13 dans f(x)
-
Saiwen
- Membre Naturel
- Messages: 20
- Enregistré le: 26 Mai 2015, 19:48
-
 par Saiwen » 27 Mai 2015, 21:07
par Saiwen » 27 Mai 2015, 21:07
Oui mais je pense que le calcul de f(13) via le discriminant est innaproprié, autant remplacer 13 directement comme je l'ai fait dans mon 1er message
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 27 Mai 2015, 21:14
par Pisigma » 27 Mai 2015, 21:14
Saiwen a écrit:Oui mais je pense que le calcul de f(13) via le discriminant est innaproprié, autant remplacer 13 directement comme je l'ai fait dans mon 1er message
Ce n'est pas f(13) mais f(x)=13
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
