Bonjour,
pour je ne sais quelle raison, c'est la seconde fois en quelques mois que je tombe sur le même sujet/problème et que je ne parviens pas à trouver de pistes pour le résoudre.
J'ai une série de valeur qui est le résultat d'une somme de 2 séries (A:partiellement connue et B:"aléatoire") et j'aimerai retrouver la série A.
Dans un cas la série A est une constante ou une "afine" a(n) = constante ou a(n)= alpha * constante
dans le second cas la série A est une série périodique a(n) = x si n=Constante
merci
Où est ma série : décomposition de séries
9 messages
- Page 1 sur 1
Salut,
oukélélakestion ?
Texto, ça donne un peu l'impression que tu as C=A+B avec C et A connu et que tu demande comment on trouve B.
Si c'est ça la question, ça va, c'est dans mes corde : on retranche A des deux cotés et ça fait B=C-A.
Mais je sais pas pourquoi, j'ai un doute concernant le fait que ce soit ça la question :doh:
oukélélakestion ?
Texto, ça donne un peu l'impression que tu as C=A+B avec C et A connu et que tu demande comment on trouve B.
Si c'est ça la question, ça va, c'est dans mes corde : on retranche A des deux cotés et ça fait B=C-A.
Mais je sais pas pourquoi, j'ai un doute concernant le fait que ce soit ça la question :doh:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Merci ;-)
Si A,B et C sont des séries et qu'on ne connait que C et la forme que A peut avoir, là je sèche.
ex:
C1=0.5
C2=0.5
C3=1
C4=2
C5=0.8
C6=0.9
C7=35
...
Dans cet exemple, on peut imaginer une Série A qui vaut 0.5 quelque soit n, mais il y a d'autres solutions. Celle que je recherche est la série avec le A le plus grand. Une sorte de PGCD.
Si A,B et C sont des séries et qu'on ne connait que C et la forme que A peut avoir, là je sèche.
ex:
C1=0.5
C2=0.5
C3=1
C4=2
C5=0.8
C6=0.9
C7=35
...
Dans cet exemple, on peut imaginer une Série A qui vaut 0.5 quelque soit n, mais il y a d'autres solutions. Celle que je recherche est la série avec le A le plus grand. Une sorte de PGCD.
Désolé, mais je... comprend toujours pas le sens de la question (vu que c'est la même).
Donc, ben je te redonne exactement la même solution...
Si (par exemple), que
(par exemple), que  est connu et que tu cherche
est connu et que tu cherche  tel que
tel que 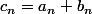 et ben ça te donne
et ben ça te donne  , ni plus... ni moins... (et en particulier strictement aucune info sur
, ni plus... ni moins... (et en particulier strictement aucune info sur  et
et  que tu peut prendre absolument comme tu veut, par exemple... très grand si ça te chante....)
que tu peut prendre absolument comme tu veut, par exemple... très grand si ça te chante....)
En fait, je comprend vraiment pas comment tu compte tirer la moindre autre information autre que B=C-A partant de C=A+B. :doh: :doh: :doh:
Que ça soit des fonction, des séries, des matrice où à peut prés n'importe quoi, ça change rien au problème Si dans C=A+B tu connait effectivement qu'un des 3, tu risque pas de trouver les deux autres (deux inconnues et une seule équation...)
P.S. pour parler de PGCD, il faut une notion de G (i.e. une relation d'ordre) et une notion de D (i.e. de divisibilité).
Et dans le cas d'une suite de réels, déjà, la notion d'ordre, c'est pas forcément clair, mais celle de divisibilité, je vois vraiment pas à quoi ça pourrait se référer.
Donc, ben je te redonne exactement la même solution...
Si
En fait, je comprend vraiment pas comment tu compte tirer la moindre autre information autre que B=C-A partant de C=A+B. :doh: :doh: :doh:
Que ça soit des fonction, des séries, des matrice où à peut prés n'importe quoi, ça change rien au problème Si dans C=A+B tu connait effectivement qu'un des 3, tu risque pas de trouver les deux autres (deux inconnues et une seule équation...)
P.S. pour parler de PGCD, il faut une notion de G (i.e. une relation d'ordre) et une notion de D (i.e. de divisibilité).
Et dans le cas d'une suite de réels, déjà, la notion d'ordre, c'est pas forcément clair, mais celle de divisibilité, je vois vraiment pas à quoi ça pourrait se référer.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
La grande difficulté reste toujours l'énoncé.
Si quelque soit n, An=Cste positive (A11=A2=A3...) et que je cherche parmi l'ensemble des solutions celle pour laquelle cette constante est la plus grande, la seule solution que je trouve c'est de calculer le min de tous les Cn. Ainsi, s'il est supérieur à 0 j'ai trouvé. Pour ce cas particulier j'ai une solution empirique.
Mais dans le cas général, si An à la forme n*Cste1 + Cste2 j'ai plus de difficulté à trouver.
Par exemples, j'ai les valeurs de la courbe ax+b+sin(x)+1 et je cherche à retrouver ax+b sachant que je ne connais pas la partie sin(x)+1; ou encore, en physique j'aurais un courant continu mélangé avec un alternatif et je souhaiterai les décomposer.
Si quelque soit n, An=Cste positive (A11=A2=A3...) et que je cherche parmi l'ensemble des solutions celle pour laquelle cette constante est la plus grande, la seule solution que je trouve c'est de calculer le min de tous les Cn. Ainsi, s'il est supérieur à 0 j'ai trouvé. Pour ce cas particulier j'ai une solution empirique.
Mais dans le cas général, si An à la forme n*Cste1 + Cste2 j'ai plus de difficulté à trouver.
Par exemples, j'ai les valeurs de la courbe ax+b+sin(x)+1 et je cherche à retrouver ax+b sachant que je ne connais pas la partie sin(x)+1; ou encore, en physique j'aurais un courant continu mélangé avec un alternatif et je souhaiterai les décomposer.
Là, je comprend... encore moins...steph401 a écrit:Laquelle cette constante est la plus grande, la seule solution que je trouve c'est de calculer le min de tous les Cn. Ainsi, s'il est supérieur à 0 j'ai trouvé. <= ??????
ou encore, en physique j'aurais un courant continu mélangé avec un alternatif et je souhaiterai les décomposer.
Déja le truc du "supérieur à 0", je vois pas d'où il sort.
Ensuite, l'analogie avec du courant en physique me parait parfaite pour comprendre... qu'il faut absolument se donner des "types" pour DEUX des éléments de la somme et pas un seul : ici, tu as C=A+B avec A continu et B alternatif alors que toi tu ne donne des contraintes que sur A donc s'est comme si tu demandait juste de décomposer le courant en un continu + n'importe quoi !!!!
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Merci ben
Tu as parfaitement compris. J'ai deux "signaux" mélangés. Un qui m'intéresse et second "parasite".
Pour le cas où le signal qui m'intéresse à une forme afine du type ax+b ton approche très simple me permet d'avancer.
il faut que je regarde maintenant si je m'en sort avec une série/fonction polynomiale d'ordre 2 ou à base exponentielle.
Comment aborderais tu le sujet, si les signaux mélangés étaient frequentiels et parasités.
J'ai regardé du côté Fourier mais je sèche un peu ( c'est loin pour moi).
Sur ce second cas je sais avoir une fréquence stable, une beaucoup moins et des parasites.
Le cas particulier de l'exercice est que l'amplitude des valeurs est inutilisable (on peut le considerer égal à un).
Steph.
Tu as parfaitement compris. J'ai deux "signaux" mélangés. Un qui m'intéresse et second "parasite".
Pour le cas où le signal qui m'intéresse à une forme afine du type ax+b ton approche très simple me permet d'avancer.
il faut que je regarde maintenant si je m'en sort avec une série/fonction polynomiale d'ordre 2 ou à base exponentielle.
Comment aborderais tu le sujet, si les signaux mélangés étaient frequentiels et parasités.
J'ai regardé du côté Fourier mais je sèche un peu ( c'est loin pour moi).
Sur ce second cas je sais avoir une fréquence stable, une beaucoup moins et des parasites.
Le cas particulier de l'exercice est que l'amplitude des valeurs est inutilisable (on peut le considerer égal à un).
Steph.
A mon avis, il te faut FORCEMENT des infos sur les deux signaux (le simple et le parasite) pour pouvoir commencer à dire des trucs.
Tu as déjà dit que pour le "simple", on peut/veut l'approcher par de l'affine (par exemple)
Après, pour le "parasite", il faut forcément supposer des trucs pour avancer.
1) Le premier truc qui me vient à l'esprit, c'est de le supposer "le plus petit possible" ce qui ramène le problème à un simple problème de régression linéaire => on veut écrire C=A+B avec B "le plus petit possible" (en général pris au sens des moindres carrés).
2) Le "parasite" est plus ou moins périodique de période connue : de nouveau régression linéaire => on veut écrire C=A+?cos(w.n)+?sin(w.n) où les deux ? sont à déterminer pour approcher "au mieux".
3) Autres options concernant la "forme" des parasites, par exemple, on sait que c'est plus ou moins aléatoire, Gaussien, avec une moyenne et un écart type connu (ou inconnu mais les calculs risquent d'être plus ardus plus dur). Si on considère que la moyenne des parasite est 0 et qu'on ne connait pas l'écart type, je me demande si on retombe pas sur une bête régression linéaire (à voir...)
Tu as déjà dit que pour le "simple", on peut/veut l'approcher par de l'affine (par exemple)
Après, pour le "parasite", il faut forcément supposer des trucs pour avancer.
1) Le premier truc qui me vient à l'esprit, c'est de le supposer "le plus petit possible" ce qui ramène le problème à un simple problème de régression linéaire => on veut écrire C=A+B avec B "le plus petit possible" (en général pris au sens des moindres carrés).
2) Le "parasite" est plus ou moins périodique de période connue : de nouveau régression linéaire => on veut écrire C=A+?cos(w.n)+?sin(w.n) où les deux ? sont à déterminer pour approcher "au mieux".
3) Autres options concernant la "forme" des parasites, par exemple, on sait que c'est plus ou moins aléatoire, Gaussien, avec une moyenne et un écart type connu (ou inconnu mais les calculs risquent d'être plus ardus plus dur). Si on considère que la moyenne des parasite est 0 et qu'on ne connait pas l'écart type, je me demande si on retombe pas sur une bête régression linéaire (à voir...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Les éléments connus:
le signal connu a une fréquence stable.
dans certain cas il peut être composé de plusieurs signaux de même fréquence avec un décalage constant
les signaux parasites sont purement aléatoires sans aucune fréquence.
ce que je souhaite retrouver c'est :
- si le signal périodique est bien présent
- la fréquence des signaux périodiques, qui peuvent varier d'un facteur 5
Je devrais peut être mettre cela dans un nouveau post.
le signal connu a une fréquence stable.
dans certain cas il peut être composé de plusieurs signaux de même fréquence avec un décalage constant
les signaux parasites sont purement aléatoires sans aucune fréquence.
ce que je souhaite retrouver c'est :
- si le signal périodique est bien présent
- la fréquence des signaux périodiques, qui peuvent varier d'un facteur 5
Je devrais peut être mettre cela dans un nouveau post.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
