alphamethyste a écrit:sauf que là pour le coup on doit travailler sur un systeme d'equation du quatrieme degré
(comme je viens de le dire c'est trompeur de penser ce que tu dit justement)
Non, c'est évidement de degré 3 (tu as 3 inconnues et je voudrais bien savoir qui pourrait bien être la prétendue 4em racine)
Et tout ce que tu raconte dans ton post à ralonge n'a rien à voir avec le problème vu que tu ne considère que des cas extrêmement particulier de sommes a+b+c, a²+b²+c², a^3+b^3+c^3, où a,b,c (donc P,Q,R) sont des entiers alors qu'ici, P,Q,R sont des réels quelconques et, à priori, a,b,c sont des nombres complexes donc ça n'a aucun rapport avec de l'arithmétique sur Z.
mathelot a écrit:... utiliser la théorie de Cardan avec
le discriminant
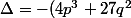)
, cette théorie indique sous quelles conditions les trois racines du polynôme de degré trois, sont réelles.
Non, ici, ça ne donnera rien d'utile : si on n'avais pas l'hypothèse extrêmement restrictive "
...n'ayant pas le même module" on ne pourrait rien conclure.
Par exemple, a=1, b=j, c=j² donnent bien P,Q,R réels et ce qui "élimine" cette solution, c'est que j et j² ont même module, et ça n'a rien à voir avec le discriminant du polynôme de 3em degré.
