Equation de graphique
25 messages
- Page 1 sur 2 - 1, 2
Equation de graphique
Bonjour à tous,
Je viens sur ce forum car j'ai un soucis.
Je tiens à préciser que je ne suis plus étudiant depuis bien longtemps, mais j'ai quelque bon reste.
Explication je suis entrain de développer un programme informatique de récupération de donnée (Sonde, Capteur,...) et je génére un ou des graphique avec les mesures.
J'aimerai avoir la possibilité de générer les équations relative au différentes courbes générées.
De plus j'aimerai les équations, d'ordre 2,3 et 4. Mais également définir les écart-type(sur ce point j'ai ma solution non testé encore).
Mes questions:
- Comment puis je faire la résolution du système avec divers point d'une courbe et en retiré les équations?
ou
- Comment faire pour avoir les équations?
- Faut il d'abord savoir le type de graph pour établir léquation ou cela peut être réalisé tel que?
Merci d'avance.
Je viens sur ce forum car j'ai un soucis.
Je tiens à préciser que je ne suis plus étudiant depuis bien longtemps, mais j'ai quelque bon reste.
Explication je suis entrain de développer un programme informatique de récupération de donnée (Sonde, Capteur,...) et je génére un ou des graphique avec les mesures.
J'aimerai avoir la possibilité de générer les équations relative au différentes courbes générées.
De plus j'aimerai les équations, d'ordre 2,3 et 4. Mais également définir les écart-type(sur ce point j'ai ma solution non testé encore).
Mes questions:
- Comment puis je faire la résolution du système avec divers point d'une courbe et en retiré les équations?
ou
- Comment faire pour avoir les équations?
- Faut il d'abord savoir le type de graph pour établir léquation ou cela peut être réalisé tel que?
Merci d'avance.
Salut,
La question est vaste et les réponses... diverses.
A priori, vu du coté matheux, je pense que ta "courbe que tu connais", c'est en fait la donné d'un nombre fini N (éventuellement grand) de points.
Du point de vu "pure matheux", il y a une énorme infinité de fonctions (très différentes les unes des autres) qui passent exactement par ces N points. Par exemple, il y a un unique polynôme de degré inférieur <=N-1 mais une infinité de polynômes de degré <=N passant par les N points.
Donc pour le moment, rien d'utilisable dans la pratique (sauf très éventuellement le calcul du fameux polynôme de degrés <=N-1, mais c'est quasi systématiquement sans intérêt dans les cas concrets)
Dans un cas comme celui dont tu parle, a ma connaissance, ce qu'on fait par contre fréquemment, c'est de se donner un ensemble de fonctions dépendant de paramètres (fonction linéaires, affines, polynôme de degré 2, fonction exponentielles, sinusoïdes,etc...) qui correspondent à ce qu'on attend comme type de résultat sur le plan théorique, puis on cherche à évaluer la valeur des paramètres de façon à ce que la courbe soit "le plus proche possible" des N points donnés. L'exemple le plus classique est celui de la "régression linéaire" où on cherche à approximer par des fonction affines.
C'est plutôt ce genre de truc que tu cherche ?
Si oui, tu as une idée de la "formule générale" de tes courbes ?
EDIT : je pense que ça répond à ta question
A la limite, tu peut te donner plusieurs "types" d'équations puis chercher dans quel "type" tu as la meilleure approximation, mais si les "types" sont très différents, je sais pas si c'est bien pertinent au niveau logique (a mon sens, on ne cherche pas "au hasard" une relation entre deux quantités, mais on a d'abord une idée de relation PUIS on vérifie que c'est cohérent avec les expériences, mais c'est peut-être un point de vue de "mateux théorique")
La question est vaste et les réponses... diverses.
A priori, vu du coté matheux, je pense que ta "courbe que tu connais", c'est en fait la donné d'un nombre fini N (éventuellement grand) de points.
Du point de vu "pure matheux", il y a une énorme infinité de fonctions (très différentes les unes des autres) qui passent exactement par ces N points. Par exemple, il y a un unique polynôme de degré inférieur <=N-1 mais une infinité de polynômes de degré <=N passant par les N points.
Donc pour le moment, rien d'utilisable dans la pratique (sauf très éventuellement le calcul du fameux polynôme de degrés <=N-1, mais c'est quasi systématiquement sans intérêt dans les cas concrets)
Dans un cas comme celui dont tu parle, a ma connaissance, ce qu'on fait par contre fréquemment, c'est de se donner un ensemble de fonctions dépendant de paramètres (fonction linéaires, affines, polynôme de degré 2, fonction exponentielles, sinusoïdes,etc...) qui correspondent à ce qu'on attend comme type de résultat sur le plan théorique, puis on cherche à évaluer la valeur des paramètres de façon à ce que la courbe soit "le plus proche possible" des N points donnés. L'exemple le plus classique est celui de la "régression linéaire" où on cherche à approximer par des fonction affines.
C'est plutôt ce genre de truc que tu cherche ?
Si oui, tu as une idée de la "formule générale" de tes courbes ?
EDIT : je pense que ça répond à ta question
donc oui : il faut d'abord savoir "où" on va chercher les équations.Hybride76 a écrit: - Faut il d'abord savoir le type de graph pour établir léquation ou cela peut être réalisé tel que?
A la limite, tu peut te donner plusieurs "types" d'équations puis chercher dans quel "type" tu as la meilleure approximation, mais si les "types" sont très différents, je sais pas si c'est bien pertinent au niveau logique (a mon sens, on ne cherche pas "au hasard" une relation entre deux quantités, mais on a d'abord une idée de relation PUIS on vérifie que c'est cohérent avec les expériences, mais c'est peut-être un point de vue de "mateux théorique")
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
La question est vaste et les réponses... diverses.
A priori, vu du coté matheux, je pense que ta "courbe que tu connais", c'est en fait la donné d'un nombre fini N (éventuellement grand) de points.
Du point de vu "pure matheux", il y a une énorme infinité de fonctions (très différentes les unes des autres) qui passent exactement par ces N points. Par exemple, il y a un unique polynôme de degré inférieur <=N-1 mais une infinité de polynômes de degré <=N passant par les N points.
Donc pour le moment, rien d'utilisable dans la pratique (sauf très éventuellement le calcul du fameux polynôme de degrés <=N-1, mais c'est quasi systématiquement sans intérêt dans les cas concrets)
Dans un cas comme celui dont tu parle, a ma connaissance, ce qu'on fait par contre fréquemment, c'est de se donner un ensemble de fonctions dépendant de paramètres (fonction linéaires, affines, polynôme de degré 2, fonction exponentielles, sinusoïdes,etc...) qui correspondent à ce qu'on attend comme type de résultat sur le plan théorique, puis on cherche à évaluer la valeur des paramètres de façon à ce que la courbe soit "le plus proche possible" des N points donnés. L'exemple le plus classique est celui de la "régression linéaire" où on cherche à approximer par des fonction affines.
C'est plutôt ce genre de truc que tu cherche ?
Si oui, tu as une idée de la "formule générale" de tes courbes ?
EDIT : je pense que ça répond à ta question donc oui : il faut d'abord savoir "où" on va chercher les équations.
A la limite, tu peut te donner plusieurs "types" d'équations puis chercher dans quel "type" tu as la meilleure approximation, mais si les "types" sont très différents, je sais pas si c'est bien pertinent au niveau logique (a mon sens, on ne cherche pas "au hasard" une relation entre deux quantités, mais on a d'abord une idée de relation PUIS on vérifie que c'est cohérent avec les expériences, mais c'est peut-être un point de vue de "mateux théorique")
Ceci me suggére une question : l'équation la plus générale d'une cubique est
Ceci veut dire que par 9 points passe une cubique et une seule.
Or, 2 cubiques peuvent se couper en 9 points (3 X 3), ce qui veut dire que par 9 points peuvent passer (au moins) 2 cubiques.
Où est l'erreur de raisonnement ?
Pythales a écrit:Ceci me suggére une question : l'équation la plus générale d'une cubique estsoient 9 coefficients à déterminer.
Ceci veut dire que par 9 points passe une cubique et une seule.
Or, 2 cubiques peuvent se couper en 9 points (3 X 3), ce qui veut dire que par 9 points peuvent passer (au moins) 2 cubiques.
Où est l'erreur de raisonnement ?
Je suis pas sûr à 100%, (mais 97% on va dire... :zen: )
à mon avis, ça provient du fait que, lorsque tu prend deux cubiques "au pif", elle vont effectivement se couper en 9 points (dans un corps algébriquement clos et modulo qu'il y ait pas de racines doubles) MAIS ces 9 points, si tu les injecte dans le système linéaire à 9 inconnues consistant à déterminer les "paramètres" des cubiques qui passent par ces 9 points, ça te fait systématiquement un système a une infinité de solution (en particulier, le déterminant du système est nul) : tes 9 points ne sont pas "quelconques" (contrairement aux deux cubiques de départ)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Faisons un essai avec du "plus petit" pour voir :
On considère les courbes d'équation y=ax²+b (j'ai bien dit que je prenais "petit"... :marteau:)
Équation de degré 2 (en x) => en général 2 points d'intersection.
2 paramètres (linéaire) => en général il passe une unique de ces courbes par deux points du plan.
Deux courbes au pif : y=cx²+d et y=ex²+f -> pts d'intersection) et
et =(-x_1,y_1)) (sans se faire c... avec les cas particuliers)
(sans se faire c... avec les cas particuliers)
Système à résoudre pour trouver les courbes y=ax²+b passant par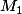 et
et 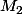 :
:  -> ça déconne : c'est deux fois la même équation...
-> ça déconne : c'est deux fois la même équation...
On considère les courbes d'équation y=ax²+b (j'ai bien dit que je prenais "petit"... :marteau:)
Équation de degré 2 (en x) => en général 2 points d'intersection.
2 paramètres (linéaire) => en général il passe une unique de ces courbes par deux points du plan.
Deux courbes au pif : y=cx²+d et y=ex²+f -> pts d'intersection
Système à résoudre pour trouver les courbes y=ax²+b passant par
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Faisons un essai avec du "plus petit" pour voir :
On considère les courbes d'équation y=ax²+b (j'ai bien dit que je prenais "petit"... :marteau:)
Équation de degré 2 (en x) => en général 2 points d'intersection.
2 paramètres (linéaire) => en général il passe une unique de ces courbes par deux points du plan.
Deux courbes au pif : y=cx²+d et y=ex²+f -> pts d'intersectionet
(sans se faire c... avec les cas particuliers)
Système à résoudre pour trouver les courbes y=ax²+b passant paret
:
-> ça déconne : c'est deux fois la même équation...
Bien vu. En fait je connaissais la réponse, mais c'était pour enrichir le débat.
Mais cela nous éloigne de la question initiale...
Suite#1
Tout d'abord merci pour ces réponses.
Sachez, que je me suis vite vu perdu avec vos réponses, malgrè mais connaissance minime.
Bref en tout cas suite au information de "Ben314":
Je ne connais pas la forme ni le type des courbes et graphiques qui sera généré, donc pour savoir comment faire cela est difficile.
Après je peux effectivement prendre "masque" ou "image" type pour savoir qu'elle genre de courbe j'ai.
Mais là Pb aussi je ne connais pas toutes les formes d'équations existante. ( ax+b, ax²+x+c,....).
Après l'autre soucis c'est de faire une approximation entre deux.
La solution basique à laquelle je pensais c'est faire une interpolation sur l'ensemble des points pour avoir une approximation.
Pour "Pythales" désolés, mais l'idée me semblait bonne mais tu m'as vite perdu.
Donc si vous avez d'autre idée ou solution qui me permettra d'avancer, je vous en remercie par avance.
Sachez, que je me suis vite vu perdu avec vos réponses, malgrè mais connaissance minime.
Bref en tout cas suite au information de "Ben314":
Je ne connais pas la forme ni le type des courbes et graphiques qui sera généré, donc pour savoir comment faire cela est difficile.
Après je peux effectivement prendre "masque" ou "image" type pour savoir qu'elle genre de courbe j'ai.
Mais là Pb aussi je ne connais pas toutes les formes d'équations existante. ( ax+b, ax²+x+c,....).
Après l'autre soucis c'est de faire une approximation entre deux.
La solution basique à laquelle je pensais c'est faire une interpolation sur l'ensemble des points pour avoir une approximation.
Pour "Pythales" désolés, mais l'idée me semblait bonne mais tu m'as vite perdu.
Donc si vous avez d'autre idée ou solution qui me permettra d'avancer, je vous en remercie par avance.
Normalement (en tout cas à mon sens, après c'est effectivement discutable), c'est le "modèle théorique" qui doit te dire que tes courbes, on peut supposer qu'elles correspondront plutôt telle ou tel type de formule.
Pour te donner un exemple couillon, si tu relève des températures au fil des heures qui passent, tu devrait plutôt avoir des truc avec plus ou moins des "périodes" (jour/nuits) donc à priori, tu cherchera plutôt des formules avec les fonction périodiques (cos et sin en l'occurrence) si c'est des truc plus ou moins connu comme ayant des croissances exponentielle dans la théorie, ben tu va "taper" dans les fonction exponentielles.
Quand on sait pas trop quoi prendre, en math, on se rabat souvent sur le "plus simple", c'est à dire les polynômes, mais de quel degrè ? Trop petit -> ça approxime mal et trop gros -> calcul long et résultat des fois catastrophique dans les zones où on a peu (ou pas) de valeurs.
Donc c'est un pis-aller (mais si on a aucune idée, on se rabat là dessus...)
Après, concernant le calcul de la "meilleure" courbe parmi la famille qu'on s'est donné, il me semble que la méthode la plus fréquemment utilisé est encore celle des "moindres carrés" qui, depuis Gauss et la fameuse comète Cérès a fait ses preuves.
Pour te donner un exemple couillon, si tu relève des températures au fil des heures qui passent, tu devrait plutôt avoir des truc avec plus ou moins des "périodes" (jour/nuits) donc à priori, tu cherchera plutôt des formules avec les fonction périodiques (cos et sin en l'occurrence) si c'est des truc plus ou moins connu comme ayant des croissances exponentielle dans la théorie, ben tu va "taper" dans les fonction exponentielles.
Quand on sait pas trop quoi prendre, en math, on se rabat souvent sur le "plus simple", c'est à dire les polynômes, mais de quel degrè ? Trop petit -> ça approxime mal et trop gros -> calcul long et résultat des fois catastrophique dans les zones où on a peu (ou pas) de valeurs.
Donc c'est un pis-aller (mais si on a aucune idée, on se rabat là dessus...)
Après, concernant le calcul de la "meilleure" courbe parmi la famille qu'on s'est donné, il me semble que la méthode la plus fréquemment utilisé est encore celle des "moindres carrés" qui, depuis Gauss et la fameuse comète Cérès a fait ses preuves.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Encore merci pour ces explications.
Par contre là je vais vraiment demander des explication limite un cours sur : "moindres carrés" car je ne connais absolument pas. Donc c'est le néant totale pour moi.
Donc si une âme charitable peux m'expliquer simplement, cela m'aiderai grandement.
Merci d'avance.
Par contre là je vais vraiment demander des explication limite un cours sur : "moindres carrés" car je ne connais absolument pas. Donc c'est le néant totale pour moi.
Donc si une âme charitable peux m'expliquer simplement, cela m'aiderai grandement.
Merci d'avance.
bonjour,
j'aiguillerai bien Hybride76 vers les courbes de Bézier et les B-splines,
le souci, c'est que je ne connais pas suffisamment ces deux théories.
Au niveau des courbes de Bézier,il me semble, que ce sont des barycentres
de polynômes qui sont construits à partir de points de contrôle, fixés,
bien en dehors du voisinage de la courbe. Comment
dériver (déduire) ces points de contrôle de la matrice de points initiale ?
j'aiguillerai bien Hybride76 vers les courbes de Bézier et les B-splines,
le souci, c'est que je ne connais pas suffisamment ces deux théories.
Au niveau des courbes de Bézier,il me semble, que ce sont des barycentres
de polynômes qui sont construits à partir de points de contrôle, fixés,
bien en dehors du voisinage de la courbe. Comment
dériver (déduire) ces points de contrôle de la matrice de points initiale ?
Hybride76 a écrit:Encore merci pour ces explications.
Par contre là je vais vraiment demander des explication limite un cours sur : "moindres carrés" car je ne connais absolument pas.
regarde ce doc de deux pages là:
Rubrique Analyse: document droite d'ajustement
Progression :-)
Bonjour,
Tout d'abord encore merci pour vos conseils.
Je me suis penché sur la solution des moindres carrées.
La progression est en marche ;-)
Je m'explique :
J'ai réussi par calcul a redéfinir l'équation de données que j'avais. Cool oui et non, car je n'arrive à avoir que la version linéaire ou affine ax+b.
Avec mes points j'ai réussi a avoir l'équation + R². J'ai aussi calcul l'écart-type et l'erreur type.
Donc je reviens vers vous afin d'avoir un soutien pour réussir a définir les équation d'ordre 2 et 3, j'ai revu mes choix à la baisse au vue de mes capacités.
durant mes rechercher j'ai pu voir qu'il y avait plusieurs méthodes pour calcul l'équation d'un moindre carré non linéaire. Mais personnellement je suis perdu avec tel ou tel méthode, de plus après avoir essayé de comprendre je me suis vite retrouvé dans le flou.
Donc si quelqu'un pouvais me guider et m'expliquer étape par étape afin de pouvoir réussi a comprendre la méthode de réalisation de la définition d'une équation avec les moindre carrée non linéaire.
Je donne si dessous les données que j'ai utilisé pour l'équation de type linéaire.
x y
-30 108
-20 57
-10 15
0 -20
10 -45
20 -62
30 -70
40 -70
50 -61
60 -44
70 -19
Merci d'avance.
Cordialement.
Tout d'abord encore merci pour vos conseils.
Je me suis penché sur la solution des moindres carrées.
La progression est en marche ;-)
Je m'explique :
J'ai réussi par calcul a redéfinir l'équation de données que j'avais. Cool oui et non, car je n'arrive à avoir que la version linéaire ou affine ax+b.
Avec mes points j'ai réussi a avoir l'équation + R². J'ai aussi calcul l'écart-type et l'erreur type.
Donc je reviens vers vous afin d'avoir un soutien pour réussir a définir les équation d'ordre 2 et 3, j'ai revu mes choix à la baisse au vue de mes capacités.
durant mes rechercher j'ai pu voir qu'il y avait plusieurs méthodes pour calcul l'équation d'un moindre carré non linéaire. Mais personnellement je suis perdu avec tel ou tel méthode, de plus après avoir essayé de comprendre je me suis vite retrouvé dans le flou.
Donc si quelqu'un pouvais me guider et m'expliquer étape par étape afin de pouvoir réussi a comprendre la méthode de réalisation de la définition d'une équation avec les moindre carrée non linéaire.
Je donne si dessous les données que j'ai utilisé pour l'équation de type linéaire.
x y
-30 108
-20 57
-10 15
0 -20
10 -45
20 -62
30 -70
40 -70
50 -61
60 -44
70 -19
Merci d'avance.
Cordialement.
Je suis pas certain de bien comprendre où tu en est exactement :
Si ce que tu cherche, c'est à approximer tes courbes par des polynômes de degré 2 ou 3 ou... plus (fixé d'avance bien sûr), c'est encore de "l'interpolation linéaire" : ici, le terme "linéaire" ne fait pas référence aux fonction x->f(x) avec lesquelles on approxime (rien qu'avec du x->ax+b ce n'est pas linéaire en c), mais aux fonctions coefficients -> f paramétrant l'ensemble dans lequel on cherche la meilleure approximation (par exemple, ax+b, c'est pas linéaire en x, mais c'est bien linéaire en a et b donc ç'est bien de "l'interpolation linéaire")
Donc, QUESTION : c'est par des polynômes que tu veut approcher ta courbe (=> c'est de l'interpolation linéaire) ou par autre chose (=> c'est éventuellement non linéaire) ?
Si ce que tu cherche, c'est à approximer tes courbes par des polynômes de degré 2 ou 3 ou... plus (fixé d'avance bien sûr), c'est encore de "l'interpolation linéaire" : ici, le terme "linéaire" ne fait pas référence aux fonction x->f(x) avec lesquelles on approxime (rien qu'avec du x->ax+b ce n'est pas linéaire en c), mais aux fonctions coefficients -> f paramétrant l'ensemble dans lequel on cherche la meilleure approximation (par exemple, ax+b, c'est pas linéaire en x, mais c'est bien linéaire en a et b donc ç'est bien de "l'interpolation linéaire")
Donc, QUESTION : c'est par des polynômes que tu veut approcher ta courbe (=> c'est de l'interpolation linéaire) ou par autre chose (=> c'est éventuellement non linéaire) ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Comme expliqué dans le premier post, je cherche a faire un graphique avec les points de mesure que je récupère. Puis générer l'équation approximative de cette courbe obtenu , et ce d'ordre 2et 3. En sachant que la forme AX+B j'ai réussi à la ressortir. Donc voila ou j'en suis.
Pour répondre à BEN314, c'est par autre chose, linéaire et non linéaire.
Encore merci pour votre aide.
Pour répondre à BEN314, c'est par autre chose, linéaire et non linéaire.
Encore merci pour votre aide.
C'est quoi que tu appelle "l'ordre" ?Hybride76 a écrit:...Puis générer l'équation approximative de cette courbe obtenu , et ce d'ordre 2 et 3...
En fait, j'ai toujours pas bien compris où tu en était...
Tu veut approximer avec des polynômes de degré 2 ou/et 3 ou c'est autre chose ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:C'est quoi que tu appelle "l'ordre" ?
En fait, j'ai toujours pas bien compris où tu en était...
Tu veut approximer avec des polynômes de degré 2 ou/et 3 ou c'est autre chose ?
en effet qu en je dis ordre 2 ou 3 c est approximatif des polynômes de degré 2 ou 3. désolé de n être pas assez Clair. donc je te confirme que je chercher à avoir les équations polynomial de degré 2 ou et 3. Encore merci de votre aide
Dans ce cas, c'est simplement de la régression linéaire.
Mettons que tes points c'est les) avec
avec 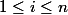 et que tu cherche par exemple le polynôme
et que tu cherche par exemple le polynôme =a+bx+cx^2+dx^3) qui approche au mieux au sens des moindres carrés.
qui approche au mieux au sens des moindres carrés.
Ca veut dire que tu cherche à minimiser la fonction=\frac{1}{n}\sum_{i=1}^n(a+bx_i+cx_i^2+dx_i^3-y_i)^2) (qui est une fonction dépendant de a,b,c,d et de rien d'autre vu que les
(qui est une fonction dépendant de a,b,c,d et de rien d'autre vu que les  et les
et les  sont connus).
sont connus).
Comme je sais pas si tu as vu les fonction de plusieurs variable donc on va faire comme si... non...
Donc, pour minimiser le bidule, on le regarde comme une fonction d'une seule variable, par exemple a en considérant que b,c,d ne bougent pas : la fonction est alors une bête fonction polynôme du second degré (en a) tel qu'on les vois au Lycée dont la courbe est une parabole tournée "vers le haut" (vu que f est clairement toujours positive).
Elle admet donc un unique minimum qui est atteint lorsque la dérivée en a s'annule, c'est à dire lorsque (dérivation en considérant que la variable est a et en utilisant (u²)'=2u'u) :
=0)
En faisant exactement pareil, mais en considérant que c'est b ou c ou d qui "bouge", (donc en dérivant par rapport à b,c ou d) on obtient
=0)
=0)
=0)
Pour simplifier ces équation, en général, on pose=\frac{1}{n}\sum_{i=1}^nx_i^k) et
et =\frac{1}{n}\sum_{i=1}^nx_i^ky_i) (quantités parfaitement calculable en partant des données de base). on obtient alors les 4 équations suivantes :
(quantités parfaitement calculable en partant des données de base). on obtient alors les 4 équations suivantes :
\ \ +cE(X^2)+dE(X^3)=E(Y))
\ \ +bE(X^2)+cE(X^3)+dE(X^4)=E(XY))
+bE(X^3)+cE(X^4)+dE(X^5)=E(X^2Y))
+bE(X^4)+cE(X^5)+dE(X^6)=E(X^3Y))
Qui est un bête système linéaire de 4 équations à 4 inconnues (a,b,c,d) qu'on s'empresse de résoudre pour avoir les solutions.
Evidement, on procèderais exactement de la même façon si on cherchais un polynôme de degré <=36 ou si on cherchais par exemple à approximer par une fonction de la forme=ax^5+b\cos(x)+c\ln(x)+d\text{ArcTan}(x)) qui est linéaire en a,b,c,d : ça se ramènerais à un simple système linéaire en a,b,c,d.
qui est linéaire en a,b,c,d : ça se ramènerais à un simple système linéaire en a,b,c,d.
Un truc qui ne serait pas directement linéaire, c'est si tu cherchais par exemple à approximer par une fonction de la forme=ax^b) avec comme inconnues a et b (mais en fait dans ce cas particulier là, on peut se ramener à du linéaire via la fonction logarithme mais ce n'est plus tout à fait la même chose qu'on minimise en fait...)
avec comme inconnues a et b (mais en fait dans ce cas particulier là, on peut se ramener à du linéaire via la fonction logarithme mais ce n'est plus tout à fait la même chose qu'on minimise en fait...)
Mettons que tes points c'est les
Ca veut dire que tu cherche à minimiser la fonction
Comme je sais pas si tu as vu les fonction de plusieurs variable donc on va faire comme si... non...
Donc, pour minimiser le bidule, on le regarde comme une fonction d'une seule variable, par exemple a en considérant que b,c,d ne bougent pas : la fonction est alors une bête fonction polynôme du second degré (en a) tel qu'on les vois au Lycée dont la courbe est une parabole tournée "vers le haut" (vu que f est clairement toujours positive).
Elle admet donc un unique minimum qui est atteint lorsque la dérivée en a s'annule, c'est à dire lorsque (dérivation en considérant que la variable est a et en utilisant (u²)'=2u'u) :
En faisant exactement pareil, mais en considérant que c'est b ou c ou d qui "bouge", (donc en dérivant par rapport à b,c ou d) on obtient
Pour simplifier ces équation, en général, on pose
Qui est un bête système linéaire de 4 équations à 4 inconnues (a,b,c,d) qu'on s'empresse de résoudre pour avoir les solutions.
Evidement, on procèderais exactement de la même façon si on cherchais un polynôme de degré <=36 ou si on cherchais par exemple à approximer par une fonction de la forme
Un truc qui ne serait pas directement linéaire, c'est si tu cherchais par exemple à approximer par une fonction de la forme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Encore merci pour ces explications.
Je suis quelque peu perdu avec ton explication. tu vas vite comprendre ca fait plus de 11 ans que j'ai quitté le banc des écoles donc là perso c'est dur dur.
Donc peux tu essayer de me donner un exemple existant ou repartir des données, mi a disposition plus haut. Afin de me guider sur la méthode ( étape par étape) si possible. Je n'attends pas une réponse direct mais la méthodologie de réalisation afin que je comprenne, puis réussir à le retranscrire pour réaliser mon projet.
en parallèle je continue mes recherche pour la compréhension du procédé que tu as proposé.
Encore merci.
Je suis quelque peu perdu avec ton explication. tu vas vite comprendre ca fait plus de 11 ans que j'ai quitté le banc des écoles donc là perso c'est dur dur.
Donc peux tu essayer de me donner un exemple existant ou repartir des données, mi a disposition plus haut. Afin de me guider sur la méthode ( étape par étape) si possible. Je n'attends pas une réponse direct mais la méthodologie de réalisation afin que je comprenne, puis réussir à le retranscrire pour réaliser mon projet.
en parallèle je continue mes recherche pour la compréhension du procédé que tu as proposé.
Encore merci.
Ben... je vois franchement pas ce que je peut dire de plus... si tu veut faire par exemple du degrés 2, tu met tes données dans un tableur :
X Y
-30 108
-20 57
-10 15
0 -20
10 -45
20 -62
30 -70
40 -70
50 -61
60 -44
70 -19
Tu rajoute des colonnes X^2, X^3, X^4 , XY, X^2Y que tu fait calculer automatiquement par le tableur, puis tu lui
demande de faire les moyennes de chacune de 7 colonnes : c'est ça les E(X^k) et E(X^kY) du post çi dessus,
Puis tu copie (automatiquement) plus loin dans le tableur la matrice&E(X^2)\cr E(X)&E(X^2)&E(X^3)\cr E(X^2)&E(X^3)&E(X^4)}\right)) ainsi que le vecteur colonne
ainsi que le vecteur colonne \cr E(XY)\cr E(X^2Y)\right))
Là, par exemple, ça donne) et
et ) , puis tu lui demande d'inverser la matrice et de multiplier l'inverse par le vecteur colonne pour résoudre le système (y'a pt'èt moyen de faire autrement : j'utilise quasiment jamais de tableurs...)
, puis tu lui demande d'inverser la matrice et de multiplier l'inverse par le vecteur colonne pour résoudre le système (y'a pt'èt moyen de faire autrement : j'utilise quasiment jamais de tableurs...)
Là, ça donne) et ça te dit que le polynôme de degré 2 qui approxime le mieux, c'est
et ça te dit que le polynôme de degré 2 qui approxime le mieux, c'est =0.042587\,X^2-2.96895\,X-19.425) (qui est quasiment égal à la série de départ) épicétou...
(qui est quasiment égal à la série de départ) épicétou...
X Y
-30 108
-20 57
-10 15
0 -20
10 -45
20 -62
30 -70
40 -70
50 -61
60 -44
70 -19
Tu rajoute des colonnes X^2, X^3, X^4 , XY, X^2Y que tu fait calculer automatiquement par le tableur, puis tu lui
demande de faire les moyennes de chacune de 7 colonnes : c'est ça les E(X^k) et E(X^kY) du post çi dessus,
Puis tu copie (automatiquement) plus loin dans le tableur la matrice
Là, par exemple, ça donne
Là, ça donne
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Suite
Bonsoir,
Encore merci pour ton aide, cela me semble plus clair.
En suivant tes explications j'arrive à retrouvé :
1 20 1400 -19,18181818
20 1400 68000 -1649,090909
1400 68000 4340000 -44254,54545
Après tu demande de faire l'inversion de la matrice et j'obtiens :
1,861538462 0,010769231 -0,000769231
0,010769231 0,003051282 -5,12821E-05
-0,000769231 -5,12821E-05 1,28205E-06
Pour avoir ccette matrive inversé, je suis passé par le Table dans mon cas fx = {INVERSMAT(tableau contenant des informations)}
Tu me dis ensuite de multiplier cette matrice inverse par 4$\left(\matrix{-19.18\cr -1649.09\cr
-44254.54}\right).
j'ai chercher comment faire et j'ai trouvé cette méthode :
A1 B1 C1 | X
A2 B2 C2 | Y
A3 B3 C3 | Z
=> A1*X, A2*X, A3 *X
=> B1*X, B2*X, B3 *X
=> C1*X, C2*X, C3 *X
Mais par cette méthode je ne retombe pas sur le résultat.
Peux tu me dire dans un premier temps si la matrice inversé est bonne et ou se trouve mon ou mes erreurs. Je chercher en parallèle, ou est mon erreur.
Encore merci.
Encore merci pour ton aide, cela me semble plus clair.
En suivant tes explications j'arrive à retrouvé :
1 20 1400 -19,18181818
20 1400 68000 -1649,090909
1400 68000 4340000 -44254,54545
Après tu demande de faire l'inversion de la matrice et j'obtiens :
1,861538462 0,010769231 -0,000769231
0,010769231 0,003051282 -5,12821E-05
-0,000769231 -5,12821E-05 1,28205E-06
Pour avoir ccette matrive inversé, je suis passé par le Table dans mon cas fx = {INVERSMAT(tableau contenant des informations)}
Tu me dis ensuite de multiplier cette matrice inverse par 4$\left(\matrix{-19.18\cr -1649.09\cr
-44254.54}\right).
j'ai chercher comment faire et j'ai trouvé cette méthode :
A1 B1 C1 | X
A2 B2 C2 | Y
A3 B3 C3 | Z
=> A1*X, A2*X, A3 *X
=> B1*X, B2*X, B3 *X
=> C1*X, C2*X, C3 *X
Mais par cette méthode je ne retombe pas sur le résultat.
Peux tu me dire dans un premier temps si la matrice inversé est bonne et ou se trouve mon ou mes erreurs. Je chercher en parallèle, ou est mon erreur.
Encore merci.
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
