Topologie : Densité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 02 Mai 2015, 20:55
par Ncdk » 02 Mai 2015, 20:55
Bonsoir
Soit

l'ensemble des suites
_{n \in N})
avec
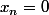
ou 1. Pour
)
et
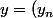)
éléments de C on pose
=\bigsum_{n=0}^{\infty} 2^{-n}|x_n - y_n|)
1) Vérifier que d définit une distance sur C. FAIT
2) Soit

l'ensemble des suites dont les termes sont nuls à partir d'un certain indice. Prouver que D est dense dans C
3) Montrer que C n'a pas de point isolé.
Je voulais faire pour la 2), essayer de prouver que D est un fermé mais je n'ai aucun idée de comment le faire, une fois que cet ensemble est fermé, je pense que vu qu'on doit prouver que D est dense dans C alors l'adhérence de D c'est C.
Mais je ne vois pas comment partir, ni même comment aboutir sur le fait que la fermeture de D c'est C.
-
Jouailleur
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Mai 2015, 16:02
-
 par Jouailleur » 02 Mai 2015, 23:07
par Jouailleur » 02 Mai 2015, 23:07
Plus simplement, considère un élément
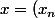)
de

et pose
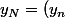)
avec

si

et

à partir du rang

.
Par définition,

.
Calcule alors
)
puis majore cette quantité. Que se passe-t-il lorsque l'on fait tendre

vers

? Conclus.
Ncdk a écrit:Bonsoir
Soit

l'ensemble des suites
_{n \in N})
avec
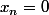
ou 1. Pour
)
et
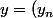)
éléments de C on pose
=\bigsum_{n=0}^{\infty} 2^{-n}|x_n - y_n|)
1) Vérifier que d définit une distance sur C. FAIT
2) Soit

l'ensemble des suites dont les termes sont nuls à partir d'un certain indice. Prouver que D est dense dans C
3) Montrer que C n'a pas de point isolé.
Je voulais faire pour la 2), essayer de prouver que D est un fermé mais je n'ai aucun idée de comment le faire, une fois que cet ensemble est fermé, je pense que vu qu'on doit prouver que D est dense dans C alors l'adhérence de D c'est C.
Mais je ne vois pas comment partir, ni même comment aboutir sur le fait que la fermeture de D c'est C.

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 03 Mai 2015, 18:54
par Ncdk » 03 Mai 2015, 18:54
Jouailleur a écrit:Calcule alors
)
puis majore cette quantité. Que se passe-t-il lorsque l'on fait tendre

vers

? Conclus.
J'ai un peu de mal, je vais déjà voir si je pars de la bonne somme :
=\bigsum_{N=n}^{\infty} 2^{-N}|x - y_N|)
Sauf que cette somme, on obtient un facteur
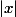
Donc du coup la somme vaut
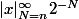
Je sais pas si je suis partit de la bonne somme pour pouvoir majorer comme tu me l'as demandé, ou je devais partir de la somme initiale puis la scindé en deux blocs donc ce qui se passe pour nN
-
Jouailleur
- Membre Naturel
- Messages: 10
- Enregistré le: 02 Mai 2015, 16:02
-
 par Jouailleur » 03 Mai 2015, 22:31
par Jouailleur » 03 Mai 2015, 22:31
Ncdk a écrit:J'ai un peu de mal, je vais déjà voir si je pars de la bonne somme :
=\bigsum_{N=n}^{\infty} 2^{-N}|x - y_N|)
Sauf que cette somme, on obtient un facteur
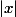
Donc du coup la somme vaut
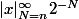
Je sais pas si je suis partit de la bonne somme pour pouvoir majorer comme tu me l'as demandé, ou je devais partir de la somme initiale puis la scindé en deux blocs donc ce qui se passe pour nN
Attention, tu n'appliques pas la définition de la distance

correctement ! Un terme

(et non

) doit apparaître dans la somme indicée par

(et non

)...
Tu dois ensuite simplement remarquer que par définition de

:
=\bigsum_{n=N}^{\infty} 2^{-n}|x_n|)
C'est cette quantité que tu majoreras facilement en notant que

ne prend que les valeurs 0 ou 1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
