Géométrie vectorielle

par **nikox6** » 03 Mai 2015, 13:16

Bonjour,

Dans le dernier exercice de mon devoir de géométrie vectorielle je dois démontrer que G, le centre de gravité d'un triangle ABC, est aux 2/3 de chaque médiane à partir du sommet. Il ne faut le démontrer que pour la médiane AA' en sachant qu'un raisonnement analogue peut être fait pour les deux autres médianes.

Je ne sait pas comment m'y prendre. Alors si vous connaissez les pistes à suivre ou la solution, aidez-moi SVP! :)

par **capitaine nuggets** » 03 Mai 2015, 13:23

Salut !

Par définition de

, on a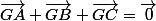

.
En faisant intervenir, grâce à la relation de Chasles le point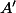

milieu de

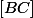, on a

,

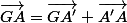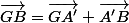et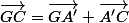

. Remplace et trouve le résultat voulu :+++:

par **nikox6** » 03 Mai 2015, 13:49

capitaine nuggets a écrit:Salut !

Par définition de , on a .
En faisant intervenir, grâce à la relation de Chasles le point milieu de , on a , et . Remplace et trouve le résultat voulu :+++:

Merci de ta réponse capitaine nuggets

Mais je bloque toujours... Je ne vois pas comment "remplacer" ?

par **capitaine nuggets** » 03 Mai 2015, 14:05

nikox6 a écrit:Merci de ta réponse capitaine nuggets
Mais je bloque toujours... Je ne vois pas comment "remplacer" ?

En remplaçant tout bêtement

,

et

par les expressions que je t'ai donné ; à la fin, tu dois obtenir

:+++:

par **nikox6** » 03 Mai 2015, 15:44

capitaine nuggets a écrit:En remplaçant tout bêtement , et par les expressions que je t'ai donné ; à la fin, tu dois obtenir :+++:

Je suis coincé ici :

par **nikox6** » 03 Mai 2015, 17:00

nikox6 a écrit:Je suis coincé ici :

C'est bon j'ai trouvé! Merci beaucoup pour ton aide Capitaine!

Géométrie vectorielle

géométrie vectorielle

Qui est en ligne