Inégalité des accroissements finis

[Tyson13]

Bonjour,

Je bloque sur la dernière question d'un exercice :

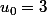
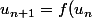Soit et avec

J'ai déjà démontré :








Je dois en déduire que :



On nous demande d'utiliser l'inégalité des accroissements finis.

Donc je pense que je dois utiliser :



Mais je n'arrive pas à le faire apparaitre dans une démonstration par récurrence.

Merci.

[Calvinator2000]

Bonsoir,

T'as déjà fait tout le travail, il ne te reste qu'à rédiger la preuve de cette inégalité par récurrence.
Vérifie que cette inégalité est vraie à un certain rang (n=1 par exemple). Suppose cette inégalité vraie au rang n et grâce à ta dernière inégalité, tu es en mesure de montrer que l'inégalité est vraie au rang n+1 donc par principe de récurrence qu'elle est vraie pour tout n.

En supposant l'inégalité vraie au rang n,



Ce qui montre la véracité de l'inégalité pour tout n entier.