Série

[Elganar]

Bonjour à tous,

Je suis bloqué au début d'un exercice...

Voici l'exo: http://i19.servimg.com/u/f19/15/79/65/23/110.png

Merci d'avance !!

[Godfrey]

Salut,

Parmi les entiers compris entre 0 et 2N+1, il y a les impairs et les pairs.
Tu peux donc voir ta somme comme d'abord la somme sur tous les impairs puis sur tous les pairs

[Elganar]

Ok je vois :)
Merci bien j'essaye d'y réfléchir !

[paquito]

Tu remarques que \bigsum_{1}{2n

[paquito]

Ok je vois
Merci bien j'essaye d'y réfléchir !

Tu remarques que

[Elganar]

Merci pour vos réponses, mais je ne vois toujours pas comment commencer :/

[Elganar]

Première question ok :)
Merci bien d'ailleurs, pour la seconde on peut dire que les deux autres termes convergent donc de même pour la série?

[Godfrey]

Si on a une égalité entre deux séries et que la série à droite est une série convergente. Alors la série de gauche sera également convergente.

[Elganar]

Mais du coup comment faire pour passer de N à +inf ?
On peut pas écrire la même égalité avec que des +inf puisque c'est faux :/

[zygomatique]

Si on a une égalité entre deux séries et que la série à droite est une série convergente. Alors la série de gauche sera également convergente.

salut

... :marteau:




la deuxième somme du membre de gauche est positive donc la première du membre de gauche est majorée par celle du membre de droite qui converge quand on fait tendre N vers l'infini

:lol3:

[Elganar]

Ah oui effectivement, présenté comme ça c'est beaucoup mieux ^^
Merci :)

[paquito]

Tu as\bigsum_{1}^{2N+1}\frac{1}{n^2}= \bigsum_{1}^{2N+1}\frac{1}{(2n+1)^2}+\frac{1}{4} \bigsum_{1}^{N}\frac{1}{n^2}, d'où à la limite \bigsum_{1}^{+oo}\frac{1}{(2n+1)^2}=\frac{\pi^2}{6}-\frac{1}{4}\frac{\pi^2}{6}=\frac{3\pi^2}{24}=\frac{\pi^2}{8}.

[mathelot]

Tu as d'où à la limite

........................

[Godfrey]

salut

... :marteau:



:lol3:

Où est le problème ? A gauche, comme à droite, on a une limite quand N tend vers l'infini, non ?

[zygomatique]

sauf que les deux séries de gauche divergent ....

[Godfrey]

Mais est convergente.

[zygomatique]

sauf qu'à gauche on a deux sommes et pas une !!!!

[Godfrey]

Ok j'ai (enfin) compris ton point de vue.
Mais comment peux-tu définir ta suite (u_n) dans prenant dans cet ordre les valeurs 1,2,3,.... -1,-2,-3,... ?
Parce que si je m'en tiens à la définition d'une série numérique,
n'est pas une série mais en est une.

[zygomatique]

le premier terme est une somme de deux séries divergentes dont la somme converge ...

le deuxième terme est une série .... trivialement convergente ....


on a les deux théorèmes suivant ::

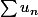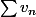si et convergent et si

alors converge et



soit

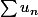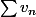si , et convergent

alors

....

[Godfrey]

Oui d'accord. Mais je ne vois pas où tu veux en venir.
Le mieux serait de reprendre depuis le début notre conversation...
J'ai dit plus haut:

Si on a une égalité entre deux séries et que la série à droite est une série convergente. Alors la série de gauche sera également convergente.
c'est -à-dire si

avec convergente alors est convergente.

Tu as essayé ensuite de me pondre un contre-exemple à cette propriété, tout à fait banale il faut l'avouer.
Dis moi plutôt en quoi ton exemple refute ce que je viens d'écrire.