Bonjour !
En fait, on voit très nettement que la fonction n'est pas continue. Pour la démonstration, je le ferais par l'absurde.
Voici ce que j'aurais mis:
On remarque d'abord que f n'est pas définie sur l'ensemble
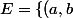 \in \mathbb{Z^*} / x=\frac{a}{2b} \})
, puisque la fonction

est définie sur
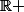
.
Ainsi, si on suppose f comme continue en 0, cela signifie que cette fonction est définie au voisinage de 0, donc sur un intervalle I du type:
[CENTER]

[/CENTER]
où

est un réel positif non nul.
Montrons que quelque soit I, il existe une partie de E incluse dans I.
On remarque que la suite
_{n \in \mathbb{n}})
définie par:
[CENTER]

[/CENTER]
est convergente et tend vers 0.
On a alors:
[CENTER]
 \Rightarrow (| u_n| <0))
[/CENTER]
Ce qui permet d'affirmer que tous les rangs de
)
appartiennent à I à partir d'un certain rang.
La fonction f n'est donc pas définie en certains points de I, ce qui est absurde.
Donc f n'est pas continue en 0.
J'espère avoir été clair et ne pas avoir fait de fautes ! :lol3:
Bonne soirée !
