Sens de variation d'une suite
15 messages
- Page 1 sur 1
Sens de variation d'une suite
Bonjour
Je doit étudier le sens de variation de de la suite (Un) avec n>0 définie par (3n-1)/(2n+2)
Voila ce que j'ai fait pour l'instant:
Soit (Un), la suite définie, pour tout n appartenant à N, par (3n-1)/(2n+2)
On sait que n>0
donc la suite (Un) à des termes strictement positifs
On à donc pour tout n appartenant à N:
[(3n+1-1)/(2n+1+2)]/[(3n-1)/(2n+2)]
Je n'arrives pas à résoudre ce calcul et je suis donc bloqué pour la suite de mon DM
Merci d'avance.
Je doit étudier le sens de variation de de la suite (Un) avec n>0 définie par (3n-1)/(2n+2)
Voila ce que j'ai fait pour l'instant:
Soit (Un), la suite définie, pour tout n appartenant à N, par (3n-1)/(2n+2)
On sait que n>0
donc la suite (Un) à des termes strictement positifs
On à donc pour tout n appartenant à N:
[(3n+1-1)/(2n+1+2)]/[(3n-1)/(2n+2)]
Je n'arrives pas à résoudre ce calcul et je suis donc bloqué pour la suite de mon DM
Merci d'avance.
Salut !
Je vois à priori trois moyens pour étudier es variations de ta suite) :
:
1) Etudier le signe de la différence .
.
2) Soit, comme il a été dit, comparer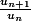 à
à  , en s'assurant bien que
, en s'assurant bien que  ne s'annule pas.
ne s'annule pas.
3) Considérer la fonction définie par
définie par =\frac{3x-1}{2x+2}) . Ta suite
. Ta suite ) étant de la forme
étant de la forme 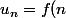) , étudier ses variations revient à étudier les variations de
, étudier ses variations revient à étudier les variations de  :+++:
:+++:
Personnellement, je te conseille la 1) ou la 2), elles marchent bien et tu as directement le résultat.
:+++:
Je vois à priori trois moyens pour étudier es variations de ta suite
1) Etudier le signe de la différence
2) Soit, comme il a été dit, comparer
3) Considérer la fonction
Personnellement, je te conseille la 1) ou la 2), elles marchent bien et tu as directement le résultat.
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Rosind a écrit:Oui et je compte utiliser la deuxième méthode ! Le problème c'est que je bloques une fois arrivé à ce calcul : [(3n+1-1)/(2n+1+2)]/[(3n-1)/(2n+2)].
J'ai beaucoup de mal à le développer pour ensuite trouver le résultat.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Rosind a écrit:Donc ça me ferait : (3n)/(2n+3) X (2n+2)/(3n-1) c'est ça ?
C'est pas que ça "ferait", ca fait effectivement ce que tu as noté : tu n'as fait que remplacer mes a,b,c,d par tes valeurs :++:
Sauf que 'y a un problème : si
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
titine a écrit:Non .
Si U(n) = (3n-1)/((2n+1) alors U(n+1) = (3(n+1)-1)/(2(n+1)+1)
Ah.. J'ai toujours fait comme ça et on ne m'a jamais rien dit ! En tout cas merci sinon j'aurais toujours fait cette faute !
Donc ça me fait:
[3(n+1)-1]/[2(n+1)+2] X (2n+2)/(3n-1)
= [3(n+1)-1]X(2n+2) / [2(n+1)+2]X(3n-1)
= [3(n+1)X2n]+[3(n+1)X2]+[-1X2n]+[-1X2] / [2(n+1)X3n]+[2(n+1)X-1]+[2X3n]+[2X-1]
= [6n(n+1)]+[6(n+1)]+[-2n]+[-2] / [6n(n+1)]+[-2(n+1)]+[6n]+[-2]
= 6(n+1)-2n / -2(n+1)+6n
C'est bien ça ?
Je ne comprends pas ton calcul.
Tout d'abord dire que U(n) = (3n-1)/(2n+2) signifie que U(...) = (3*...-1)/(2*...+2)
Ok ?
Par exemple :
U(10) = (3*10-1)/(2*10+2)
Ou : U(4238) = (3*4238-1)/(2*4238+2)
Toujours d'accord ?
Donc U(n+1) = (3*(n+1)-1)/(2*(n+1)+2) = (3n+3-1)/(2n+2+2) = (3n+2)/(2n+4)
Donc U(n+1)/U(n) = ((3n+2)/(2n+4)) * ((2n+2)/(3n-1)) = ((3n+2)(2n+2))/((2n+4)(3n-1))
= (6n²+10n+4)/(6n²+10n+4)
Comme 6n²+10n+4 > 6n²+10n+4
alors (6n²+10n+4)/(6n²+10n+4) > 1
Donc U(n+1)/U(n) > 1
Et comme de plus on a vu que U(n) > 0
Alors U(n+1) > U(n)
Donc la suite (U(n)) est croissante.
Tout d'abord dire que U(n) = (3n-1)/(2n+2) signifie que U(...) = (3*...-1)/(2*...+2)
Ok ?
Par exemple :
U(10) = (3*10-1)/(2*10+2)
Ou : U(4238) = (3*4238-1)/(2*4238+2)
Toujours d'accord ?
Donc U(n+1) = (3*(n+1)-1)/(2*(n+1)+2) = (3n+3-1)/(2n+2+2) = (3n+2)/(2n+4)
Donc U(n+1)/U(n) = ((3n+2)/(2n+4)) * ((2n+2)/(3n-1)) = ((3n+2)(2n+2))/((2n+4)(3n-1))
= (6n²+10n+4)/(6n²+10n+4)
Comme 6n²+10n+4 > 6n²+10n+4
alors (6n²+10n+4)/(6n²+10n+4) > 1
Donc U(n+1)/U(n) > 1
Et comme de plus on a vu que U(n) > 0
Alors U(n+1) > U(n)
Donc la suite (U(n)) est croissante.
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
