Polynôme système homogène

[Mane]

Bonsoir,

On considère f de classe C^;) sur R. Soient p + 1 réels distincts et p + 1 entiers 0, .
On veut établir l'existence et l'unicité d'un polynôme P(X) tel que
• deg(P) n avec n = p +
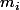
• , 0 k , 0 i p

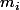
a) Soit P de degré n. On suppose que pour 0 i p et 0 k . Prouver que P est nul.
b) Expliquer pourquoi chercher P vérifiant les conditions ci-dessus revient à résoudre un système linéaire de n + 1 équations à n + 1 inconnues, les inconnues étant les coefficients de P.
c) Quelles sont les solutions homogènes de ce système ? En déduire que le système possède une unique solution.
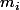
d) Lorsque tous les sont nuls, que retrouve-t-on ?

Je bloque sur la c j'aurais besoin d'aide

[L.A.]

Bonjour,

si tu écris ton système sous forme matricielle AX=B avec X le vecteur colonnes des n+1 inconnues, alors les solutions homogènes sont les solutions de AX=0. Tu sais alors que toute solution de AX=B s'écrit comme la somme d'une solution particulière fixée et d'une solution homogène quelconque.

Or si tu as fait la question a, les solutions homogènes te sont connues :zen: