Récurrence polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Mane
- Membre Naturel
- Messages: 10
- Enregistré le: 08 Avr 2015, 20:41
-
 par Mane » 08 Avr 2015, 20:45
par Mane » 08 Avr 2015, 20:45
Bonsoir
Soit
= \sum_{j=0}^n f(x_j) \prod_{k=0,j\neq k}^n \frac{X-x_k}{x_j -x_k})
Prouver par récurrence sur n que le polynôme d'interpolation de f aux points

peut s'écrire :
= a_0+ \sum_{k=1}^n a_k (X-x_0)...(X-x_{k-1}))
J'ai un problème avec l'initialisation lorsque je prends n=1 j'obtiens
d'un côté
= f(x_0)*\frac{X-x_1}{x_0 - x_1} + f(x_1) * \frac{X-x_0}{x_1 - x_0})
et de l'autre
= a_0+a_1 * (X-x_0))
Je ne trouve pas que c'est égal

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 08 Avr 2015, 20:54
par capitaine nuggets » 08 Avr 2015, 20:54
Mane a écrit:Bonsoir
Soit
= \sum_{j=0}^n f(x_j) \prod_{k=0,j\neq k}^n \frac{X-x_k}{x_j -x_k})
Prouver par récurrence sur n que le polynôme d'interpolation de f aux points

peut s'écrire :
= a_0+ \sum_{k=1}^n a_k (X-x_0)...(X-x_{k-1}))
J'ai un problème avec l'initialisation lorsque je prends n=1 j'obtiens
d'un côté
= f(x_0)*\frac{X-x_1}{x_0 - x_1} + f(x_1) * \frac{X-x_0}{x_1 - x_0})
et de l'autre
= a_0+a_1 * (X-x_0))
Je ne trouve pas que c'est égal
Salut !
Tu veux du

, donc faisons-le apparaître :
Remarque que :
[CENTER]
 \times \frac{X-x_1}{x_0 - x_1} = f(x_0) \times \frac{X-x_0+x_0-x_1}{x_0 - x_1} = f(x_0) \times \frac{X-x_0}{x_0 - x_1} + f(x_0))
[/CENTER]
:+++:
-
Pauly
- Membre Naturel
- Messages: 13
- Enregistré le: 30 Oct 2014, 11:07
-
 par Pauly » 08 Avr 2015, 21:00
par Pauly » 08 Avr 2015, 21:00
Ah oui j'avais pas vu l'astuce :)
J'ai essayé l'heridité mais je bloque aussi peux-tu m'aider stp
-
Mane
- Membre Naturel
- Messages: 10
- Enregistré le: 08 Avr 2015, 20:41
-
 par Mane » 08 Avr 2015, 21:11
par Mane » 08 Avr 2015, 21:11
capitaine nuggets a écrit:Salut !
Tu veux du

, donc faisons-le apparaître :
Remarque que :
[CENTER]
 \times \frac{X-x_1}{x_0 - x_1} = f(x_0) \times \frac{X-x_0+x_0-x_1}{x_0 - x_1} = f(x_0) \times \frac{X-x_0}{x_0 - x_1} + f(x_0))
[/CENTER]
:+++:
Merci pour votre aide

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 08 Avr 2015, 21:22
par capitaine nuggets » 08 Avr 2015, 21:22
Suppose qu'il existe

réels

tels que :
[CENTER]
 \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^n \ \frac{X-x_k}{x_j -x_k}= a_0+ \sum_{k=1}^n \ a_k (X-x_0)...(X-x_{k-1}))
,[/CENTER]
montre qu'alors, pour le rang suivant, il existe
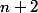
réels

tels que :
[CENTER]
 \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^{n+1} \ \frac{X-x_k}{x_j -x_k}= b_0+ \sum_{k=1}^{n+1} \ b_k (X-x_0)...(X-x_{k-1}))
.[/CENTER]
Pars de
 \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^{n+1} \ \frac{X-x_k}{x_j -x_k})
, et utilise l'hypothèse de récurrence, en remarquant que :
[CENTER]
 \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^{n+1} \ \frac{X-x_k}{x_j -x_k} = \sum_{j=0}^{n} f(x_j) \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^{n+1} \ \frac{X-x_k}{x_j -x_k} + f(x_{n+1}) \prod_{\begin{\matrix} k=0 }^{n} \ \frac{X-x_k}{x_{n+1}-x_k}=)
[/CENTER]
:+++:
-
Mane
- Membre Naturel
- Messages: 10
- Enregistré le: 08 Avr 2015, 20:41
-
 par Mane » 08 Avr 2015, 21:26
par Mane » 08 Avr 2015, 21:26
capitaine nuggets a écrit:Suppose qu'il existe

réels

tels que :
[CENTER]
 \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^n \ \frac{X-x_k}{x_j -x_k}= a_0+ \sum_{k=1}^n \ a_k (X-x_0)...(X-x_{k-1}))
,[/CENTER]
montre qu'alors, pour le rang suivant, il existe
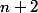
réels

tels que :
[CENTER]
 \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^{n+1} \ \frac{X-x_k}{x_j -x_k}= b_0+ \sum_{k=1}^{n+1} \ b_k (X-x_0)...(X-x_{k-1}))
.[/CENTER]
Pars de
 \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^{n+1} \ \frac{X-x_k}{x_j -x_k})
, et utilise l'hypothèse de récurrence, en remarquant que :
[CENTER]
 \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^{n+1} \ \frac{X-x_k}{x_j -x_k} = \sum_{j=0}^{n} f(x_j) \prod_{\begin{matrix} k=0 \\ j\neq k \end{matrix}}^{n+1} \ \frac{X-x_k}{x_j -x_k} + f(x_{n+1}) \prod_{\begin{\matrix} k=0 }^{n} \ \frac{X-x_k}{x_{n+1}-x_k}=)
[/CENTER]
:+++:
J'ai réussi merci beaucoup

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 08 Avr 2015, 21:41
par capitaine nuggets » 08 Avr 2015, 21:41
De rien :+++:
@+

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Avr 2015, 07:04
par Ben314 » 09 Avr 2015, 07:04
Salut,
Je ne comprend pas trop ce que vous faîtes (ou alors c'est l'énoncé que je ne comprend pas...)
Perso, pour prouver que "le polynôme d'interpolation de f aux points

peut s'écrire :
= a_0+ \sum_{k=1}^n a_k (X-x_0)...(X-x_{k-1}))
"
J'aurais (sans doute très bêtement) dit que la famille { 1 , X-x0 , (X-x0)(X-x1) , . . . , (X-x0)(X-x1)...(X-xn) } était une base de Rn[X] vu qu'elle contient un polynôme de chaque degré donc que tout polynôme de degré au plus n s'écrit sous la forme demandée.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 09 Avr 2015, 07:56
par capitaine nuggets » 09 Avr 2015, 07:56
Ben314 a écrit:Salut,
Je ne comprend pas trop ce que vous faîtes (ou alors c'est l'énoncé que je ne comprend pas...)
Son exercice demande de faire un raisonnement par récurrence.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
peut s'écrire :