Diagramme commutatif ou pas commutatif

[Aetique]

Bonjour à tous, j'ai une petite question concernant ce genre de diagramme que je ne maîtrise pas :

Soit A, X et Y trois groupes.

Supposons que l'on ait trois morphismes de groupes comme sur l'image tel que :
- et sont surjectifs
- Et est un isomorphisme de groupes.




Est-ce que le diagramme est commutatif ?
Càd est-ce que

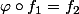
Et est-ce que


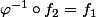
A priori je pense que non, on a trop peu d'infos pour que cela soit commutatif.. Et est-ce que ?

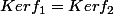
Bonnes fêtes à vous.

[Wataru]

Salut,

Je ne suis pas super doué en diagrammes mais...
Si on prend pour A Z/3Z, et pour X et Y Z/2Z. Pour phi l'application identité de Z/2Z et pour f1 et f2 :

f1(1) = 1, f1(2) = 1, f1(3) = 2
f2(1) = 1, f2(2) = 2, f2(3) = 2

On a alors toutes les conditions demandées.
Et on voit bien que (phi)o(f1)(2) = phi(1) = 1
Et f2(2) = 2

Du coup il me semble que, à part si j'ai mal compris, les deux fonctions peuvent pas vraiment être égales.

Et si mon exemple est bien valable, tu devrais avoir par la même occasion les réponses à tes questions.

[zygomatique]

salut

h = phi

h o f1 et f2 sont deux applications surjectives de A dans Y .... qui n'ont aucune raison d'être égales sans information supplémentaires

f1 et h^-1 o f2 sont .... de A dans X ... qui n'ont ....(voir la phrase au dessus) ....