Expression Algébrique & domaine de définition

[Sylich]

Bonjour, je fais une remise à niveau en Mathématiques, pour ensuite suivre un cours en BTS informatique. Je bloque à la deuxième page ... : :ptdr:

;)2x - 2 Il me dit que le domaine de définition est de [1; + &[ (désolé je ne sais pas mettre & en couché)..

Le domaine de définition doit-il être toujours positiff .

[Manny06]

Bonjour, je fais une remise à niveau en Mathématiques, pour ensuite suivre un cours en BTS informatique. Je bloque à la deuxième page ... : :ptdr:

2x - 2 Il me dit que le domaine de définition est de [1; + &[ (désolé je ne sais pas mettre & en couché)..

Le domaine de définition doit-il être toujours positiff .

si ta fonction est définie par f(x)=V(2x-2) le V désignant la racine carrée
cette fonction est définie sur R+ donc 2x-2>=0 donc x>=1

[annick]

Bonjour,
je suppose que ton expression est ;)(2x - 2) (tout est sous la racine)

Ce qu'il y a sous la racine doit toujours être positif, donc ici :

2x-2>0
2x>2
x>1

D'où ton domaine de définition.

[annick]

@ Manny06 : bonjour à toi et bravo, tu as gagné sur le fil. :lol3:

[Sylich]

D'accord, pour que la réponse soit bonne, il faut R+.
Si, c'était R- ce serait l'inverse ]-& ; 0] (dit moi que j' ai tout compris. :happy2:)

[annick]

Ce n'est pas R+ car sinon, ce serait de ]0,+00[.
Ici, c'est [1, +00[

[Robic]

Attention, l'ensemble de définition, c'est l'ensemble de définition de x, pas l'ensemble de définition de la racine carrée. Oui, la racine carrée est définie pour des nombres positifs, mais ici le nombre dans la racine est x-1, pas x tout court.

Exemples :

1) . Pour calculer la racine carrée, le nombre dans la racine, à savoir x, doit être positif. Donc x doit être positif. Donc l'ensemble de définition, c'est [0 ;+oo[.

2) Pour calculer la racine carrée, le nombre dans la racine, à savoir x-1, doit être positif. Donc x-1 doit être positif, donc 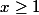. Donc l'ensemble de définition, c'est [1 ;+oo[.

3) Pour calculer la racine carrée, le nombre dans la racine, à savoir 1-x², doit être positif. Donc 1-x² doit être positif, ce qui se produit si et seulement si. Donc l'ensemble de définition, c'est [-1 ;+1].