Exo de probabilités
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 10:28
par Shew » 30 Mar 2015, 10:28
yayamat a écrit:=(3n(n+1))/2+n
=3n^2+3n/2+n
=3n^2+3n/2+2n/2
=3n^2+5n/2 merci ^^
c'est bon
Ouffff oui c'est bon :happy2:
c)E k^2 (n(n+1)(2n+1))/6
=(n(2n^2+n+2n+1))/6
=(2n^3+n^2+2n^2+n)/6
=(2n^3+3n^2+n)/6
c'est bon?
Non . On a de ce qui précède
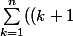^3 - k^3) = n^3 + 3n^2 + 3n)
et
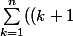^3 - k^3) = 3\sum_{k = 1}^n (k^2) + \frac{3n^2 + 5n}{2})
soit :
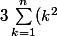 + \frac{3n^2 + 5n}{2} = n^3 + 3n^2 + 3n)
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 11:03
par yayamat » 30 Mar 2015, 11:03
3 E(k^2)=(n^3+3n^2+3n)-(3n^2+5n)/2
mtt je résous cet équation?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 11:59
par Shew » 30 Mar 2015, 11:59
yayamat a écrit:3 E(k^2)=(n^3+3n^2+3n)-(3n^2+5n)/2
mtt je résous cet équation?
Oui tout à fait, simplifiez l'expression en multipliant chaque expression par 2 de part et d'autre du signe égale .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 12:17
par yayamat » 30 Mar 2015, 12:17
ok ! ce soir je reprend
pour l'instant je suis occupé . merci beaucoup !
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 12:19
par Shew » 30 Mar 2015, 12:19
yayamat a écrit:ok ! ce soir je reprend
pour l'instant je suis occupé . merci beaucoup !
Pas de problème
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 12:19
par yayamat » 30 Mar 2015, 12:19
à ce soir*
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 17:37
par yayamat » 30 Mar 2015, 17:37
3 E(k^2)=(n^3+3n^2+3n)-(3n^2+5n)/2
3 E(k^2)=(2(n^3+3n^2+3n))/2-(3n^2+5n)/2
3 E(k^2)=(2n^3+6n^2+6n)/2 - (3n^2-5n)/2
3 E(k^2)=(2n^3+3n^2+n)/2
3 E(k^2)=(n(2n^2+3n^2+1)/2
??
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 17:37
par yayamat » 30 Mar 2015, 17:37
3 E(k^2)=(n(2n^2+3n+1)/2 ** la derniere ligne je fais une petite erreur merci
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 17:52
par Shew » 30 Mar 2015, 17:52
yayamat a écrit:3 E(k^2)=(n(2n^2+3n+1)/2 ** la derniere ligne je fais une petite erreur merci
Non c'est bon divisez par 3 des deux côtés du signe et factorisez

-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 18:06
par yayamat » 30 Mar 2015, 18:06
je n'ai pas compris ce que tu viens de dire.
3 E(k^2)=(n(2n^2+3n+1)/2
3 E(k^2)=2n^2+3n+1. ??
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 18:10
par Shew » 30 Mar 2015, 18:10
yayamat a écrit:je n'ai pas compris ce que tu viens de dire.
3 E(k^2)=(n(2n^2+3n+1)/2
3 E(k^2)=2n^2+3n+1. ??
On divise par 3 des deux côtés du signe :
}{3} = \frac{\frac{n(2n^2 + 3n + 1)}{2}}{3} \Leftrightarrow \sum_{k = 1}^n (k^2) = \frac{n(2n^2 + 3n + 1)}{6})
maintenant vous pouvez factoriser

-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 18:20
par yayamat » 30 Mar 2015, 18:20
Ah oui d'accord merci
mais comment tu peux disparaitre le nombre n =>n(2n^2+3n+1) ?
=2n^2+3n+1
=n(2n+3+1)
=n(2n+3)(n+1)??
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 18:26
par Shew » 30 Mar 2015, 18:26
yayamat a écrit:Ah oui d'accord merci
mais comment tu peux disparaitre le nombre n =>n(2n^2+3n+1) ?
=2n^2+3n+1
=n(2n+3+1)
=n(2n+3)(n+1)??
:hein: :hein: :hein:
Chez moi :
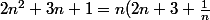)
Essayez plutot :
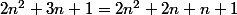
. Je vous laisse la conclusion
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 19:14
par yayamat » 30 Mar 2015, 19:14
(n(2n+3+1/n))/6
=(2n^2+3n+1)/6
=(2n^2+2n+n+1)/6
=n(2n+1)(n+2)/6
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 19:23
par Shew » 30 Mar 2015, 19:23
yayamat a écrit:(n(2n+3+1/n))/6
=(2n^2+3n+1)/6
=(2n^2+2n+n+1)/6
=n(2n+1)(n+2)/6
Oui !!! :++: :++:
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 19:26
par yayamat » 30 Mar 2015, 19:26
mais la question 3)c) en déduire que Ek^2 = (n(n+1)(2n+1))/6
moi j ai trouve n(2n+1)(n+2)/6??
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 19:42
par Shew » 30 Mar 2015, 19:42
yayamat a écrit:mais la question 3)c) en déduire que Ek^2 = (n(n+1)(2n+1))/6
moi j ai trouve n(2n+1)(n+2)/6??
Euh oui regardez votre developpement .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 19:51
par yayamat » 30 Mar 2015, 19:51
en fait c est (n(n+1)(2n+1))/6 ? pas n(2n+1)(n+2)/6
V(X)= ?? c'est la dernière question allez merci !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 108 invités