Exo de probabilités
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 18:56
par Shew » 29 Mar 2015, 18:56
yayamat a écrit:\sum_{k = 1}^n ((k + 1)^3 - k^3) = [(1 + 1)^3 - 1^3] + [(2 + 1)^3 - 2^3] + [(3 + 1)^3 - 3^3] + ... + [(n + 1)^3 - n^3]
=((1 + 1)^3 - 1^3) + ((2 + 1)^3 - 2^3)+((3+1)^3-3^3)+((n+1)^3-n^3)
=(2^3-1^3)+(3^3-2^3)+(4^3-3^3)+((n+1)^3-n^3)
=1^3+1^3+1^3+...+((n+1)^3-n^3)
Non . On imagine que le schema se répète donc :
^3 - 1^3] + [(2 + 1)^3 - 2^3] + [(3 + 1)^3 - 3^3] + ... + [(n + 1)^3 - n^3] = 2^3 - 1^3 + 3^3 - 2^3 + 4^3 - 3^3)
on remarque que le terme
^3)
annule le terme
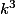
de l'expression suivante or

est la plus petite valeur donc ne peut être annulée et
^3)
est la plus grande valeur et ne peut être annulée donc on a :
^3 - 1^3] + [(2 + 1)^3 - 2^3] + [(3 + 1)^3 - 3^3] + ... + [(n + 1)^3 - n^3] = -1^3 + (n + 1)^3 = n^3 + 3n^2 + 3n + 1 - 1^3)
. Je vous laisse simplifier et conclure .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 19:33
par yayamat » 29 Mar 2015, 19:33
Shew a écrit:Non . On imagine que le schema se répète donc :
^3 - 1^3] + [(2 + 1)^3 - 2^3] + [(3 + 1)^3 - 3^3] + ... + [(n + 1)^3 - n^3] = 2^3 - 1^3 + 3^3 - 2^3 + 4^3 - 3^3)
on remarque que le terme
^3)
annule le terme
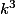
de l'expression suivante or

est la plus petite valeur donc ne peut être annulée et
^3)
est la plus grande valeur et ne peut être annulée donc on a :
^3 - 1^3] + [(2 + 1)^3 - 2^3] + [(3 + 1)^3 - 3^3] + ... + [(n + 1)^3 - n^3] = -1^3 + (n + 1)^3 = n^3 + 3n^2 + 3n + 1 - 1^3)
. Je vous laisse simplifier et conclure .
ah d'accord c'est chaud^^ :doh: merci beaucoup ! je comprends mieux maintenant.
bref
n^3 + 3n^2 + 3n + 1 - 1^3=n^3 + 3n^2 + 3n donc E((k+1)3-k3)=n3+3n2+3n.
3)b)
E((k+1)^3-k^3)=3 E k^2+(3n^2+5n)/2
=(3((1 + 1)^3 - 1^3) + (3((2 + 1)^3 - 2^3)+(3((3+1)^3-3^3)+(3(n+1)^3-n^3) (on multiplie par 3)
c'est ca ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 20:13
par Shew » 29 Mar 2015, 20:13
yayamat a écrit:ah d'accord c'est chaud^^ :doh: merci beaucoup ! je comprends mieux maintenant.
bref
n^3 + 3n^2 + 3n + 1 - 1^3=n^3 + 3n^2 + 3n donc E((k+1)3-k3)=n3+3n2+3n.
3)b)
E((k+1)^3-k^3)=3 E k^2+(3n^2+5n)/2
=(3((1 + 1)^3 - 1^3) + (3((2 + 1)^3 - 2^3)+(3((3+1)^3-3^3)+(3(n+1)^3-n^3) (on multiplie par 3)
c'est ca ?
Attendez, le meilleur reste à venir si vous trouviez l'autre compliqué :lol3:
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 20:40
par yayamat » 29 Mar 2015, 20:40
Shew a écrit:Attendez, le meilleur reste à venir si vous trouviez l'autre compliqué :lol3:
:marteau: oui je ne sais pas par quoi commencer
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 07:24
par yayamat » 30 Mar 2015, 07:24
yayamat a écrit::marteau: oui je ne sais pas par quoi commencer
UP :hein: :mur:
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 07:36
par Shew » 30 Mar 2015, 07:36
yayamat a écrit::marteau: oui je ne sais pas par quoi commencer
Pour la partie de l'esperance au tant pour moi je n'avais pas terminé le développement, vous aviez en partie raison,
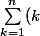 = \frac{n*(n + 1)}{2})
soit
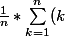 = ?)
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 07:51
par Shew » 30 Mar 2015, 07:51
Pour la 3b on décompose ainsi :
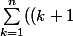^3 - k^3) = \sum_{k = 1}^n ((k^3 + 3k^2 + 3k + 1 - k^3) = \sum_{k = 1}^n (3k^2 + 3k + 1) = \\ \sum_{k = 1}^n (3k^2) + \sum_{k = 1}^n (3k) + \sum_{k = 1}^n (1) = 3*\sum_{k = 1}^n (k^2) + 3*\sum_{k = 1}^n (k) + \sum_{k = 1}^n (1))
Je vous laisse faire la suite du développement .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 07:59
par yayamat » 30 Mar 2015, 07:59
merci. d'accord.
donc
3*E(k^2)=3(1^2+2^2+3^2...+n^2)
3*E(k)=3(1+2+3+...+n)
E(1)=1+2+3+...+n
donc =>3(1^2+2^2+3^2...+n^2) + (1+2+3+...+n) + (1+2+3+...+n)
c'est bon?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 08:04
par Shew » 30 Mar 2015, 08:04
yayamat a écrit:merci. d'accord.
donc
3*E(k^2)=3(1^2+2^2+3^2...+n^2)
3*E(k)=3(1+2+3+...+n)
E(1)=1+2+3+...+n
donc =>3(1^2+2^2+3^2...+n^2) + (1+2+3+...+n) + (1+2+3+...+n)
c'est bon?
Pas besoin de développer
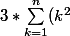)
puisqu'il est dans la question . Pour
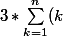)
vous avez établi que
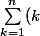 = \frac{n*(n + 1)}{2})
donc
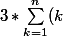 = ???)
. Pour
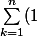)
c'est la somme (1 + 1 + 1 + 1 + ... + n) répétée n fois soit
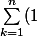 = ???)
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 08:13
par yayamat » 30 Mar 2015, 08:13
Shew a écrit:Pas besoin de développer
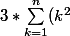)
puisqu'il est dans la question . Pour
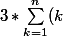)
vous avez établi que
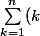 = \frac{n*(n + 1)}{2})
donc
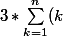 = ???)
. Pour
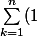)
c'est la somme (1 + 1 + 1 + 1 + ... + n) répétée n fois soit
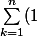 = ???)
d'accord
3*E(k^2)=((n*(n+1))^2/2)*3
3*E(k)=(n*(n+1)/2)*3
E(1)=n*(n+1)/2 ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 08:16
par Shew » 30 Mar 2015, 08:16
yayamat a écrit:d'accord
3*E(k^2)=((n*(n+1))^2/2)*3
3*E(k)=(n*(n+1)/2)*3
E(1)=n*(n+1)/2 ?
Je vous l'ai dit pour le
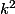
on le laisse sous la forme sigma (c'est dans l'enoncé de l'exercice), pour 3k c'est bon et pour
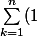)
. Pour vous aider à comprendre mettez ces sommes sous forme de produit : (1 + 1 + 1), (1 + 1 + 1 + 1), (1 + 1 + 1 + ... + n)
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 08:21
par yayamat » 30 Mar 2015, 08:21
E(1)=1*(1+1)/2
n est remplacé par 1 ?
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 08:36
par Shew » 30 Mar 2015, 08:36
yayamat a écrit:E(1)=1*(1+1)/2
n est remplacé par 1 ?
Ce n'est pas une suite arithmetique, calculer
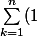)
revient à calculer
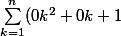)
soit :
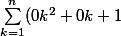 = [0*1^2 + 0*1 + 1] + [0*2^2 + 0*2 + 1] + ... + [0n^2 + 0n+ 1] = [1 + 1 + 1 + 1 + .... + 1])
Comme l'expression compte n valeurs donc on répète 1 n fois soit
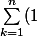 = n)
. D'après ce que vous avez trouvé on a donc :
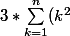 + \frac{3n(n + 1)}{2} + n)
. Dans cette expression:
}{2} + n)
développez le numérateur, ramenez tout au même dénominateur et simplifiez l'expression .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 09:09
par yayamat » 30 Mar 2015, 09:09
3*E(k^2)=pas de besoin de développer ok
3*E(k)=(n*(n+1)/2)*3=3n*(3n+3)/6 = 3n*(n+3)/2 c'est bon?
E(1)=n ok
donc => 3*E(k^2)+(3n(n+1))/2)+n
= 3*E(k^2)+ (3n(n+1))*n/2*n + (2n/2n)
= 3*E(k^2) +3n^2*(n^2+n)/2n + 2n/2n
= 3*E(k^2 +(3n^4+3n^3+2n)/2
ca va pas du tout ..
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 09:51
par Shew » 30 Mar 2015, 09:51
yayamat a écrit:3*E(k^2)=pas de besoin de développer ok
3*E(k)=(n*(n+1)/2)*3=3n*(3n+3)/6 = 3n*(n+3)/2 c'est bon?
E(1)=n ok
donc => 3*E(k^2)+(3n(n+1))/2)+n
= 3*E(k^2)+ (3n(n+1))*n/2*n + (2n/2n)
= 3*E(k^2) +3n^2*(n^2+n)/2n + 2n/2n
= 3*E(k^2 +(3n^4+3n^3+2n)/2
ca va pas du tout ..
Attention aux fautes d'etourderie, le début est bon pourquoi multiplier encore par

Pourquoi vouloir ramener à un dénominateur de 2n ???? :hum:
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 10:08
par yayamat » 30 Mar 2015, 10:08
mais n=2n/2n
tout au même dénominateur c'est 2n??
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 10:09
par Shew » 30 Mar 2015, 10:09
yayamat a écrit:mais n=2n/2n
tout au même dénominateur c'est 2n??
:doh: :doh: :doh: :doh: :doh:
}{2})
Ah Bonnnn ?????? Je signale que c'est du niveau collège (6 ème/5 ème) !!!!!!!!
Et puis
 PAS
PAS 
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 10:16
par yayamat » 30 Mar 2015, 10:16
=(3n(n+1))/2+n
=(3n(n+1))/2+2/2 c'est ca (n=n/n=1 après réduire au même dénominateur??)
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 30 Mar 2015, 10:19
par Shew » 30 Mar 2015, 10:19
yayamat a écrit:=(3n(n+1))/2+n
=(3n(n+1))/2+2/2 c'est ca (n=n/n=1 après réduire au même dénominateur??)
Je ne comprends pas votre raisonnement, essayez d'être cohérent
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 30 Mar 2015, 10:25
par yayamat » 30 Mar 2015, 10:25
=(3n(n+1))/2+n
=3n^2+3n/2+n
=3n^2+3n/2+2n/2
=3n^2+5n/2 merci ^^
c'est bon
c)E k^2 (n(n+1)(2n+1))/6
=(n(2n^2+n+2n+1))/6
=(2n^3+n^2+2n^2+n)/6
=(2n^3+3n^2+n)/6
c'est bon?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
