Comment factoriser une expression?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
chloegte
- Messages: 1
- Enregistré le: 29 Mar 2015, 14:21
-
 par chloegte » 29 Mar 2015, 14:30
par chloegte » 29 Mar 2015, 14:30
Bonjour,
Est il possible de factoriser l'expression suivante: x au cube+ 3x au carré -4 ?
Merci d'avance.

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 29 Mar 2015, 14:40
par WillyCagnes » 29 Mar 2015, 14:40
f(x)= x^3 +3x²-4=0
pour x=1 f(1)=0
donc tu peux mettre en facteur (x-1)(ax²+bx+c)= x^3+3x²-4
pour identifier les coef de meme puissance de x après developpement
a=1
b=? à chercher
c=4

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Mar 2015, 16:21
par zygomatique » 29 Mar 2015, 16:21
salut
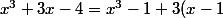 = x^3 - x^2 + x^2 - x + x - 1 + 3(x - 1) = x^2(x - 1) + x(x - 1) + 1(x - 1) + 3(x - 1) = ....)
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 16:29
par Shew » 29 Mar 2015, 16:29
zygomatique a écrit:salut
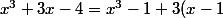 = x^3 - x^2 + x^2 - x + x - 1 + 3(x - 1) = x^2(x - 1) + x(x - 1) + 1(x - 1) + 3(x - 1) = ....)
:ptdr:
C'est
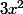
:lol3:

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 29 Mar 2015, 16:34
par zygomatique » 29 Mar 2015, 16:34
salut
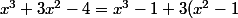 = x^3 - x^2 + x^2 - x + x - 1 + 3(x^2 - 1) = x^2(x - 1) + x(x - 1) + 1(x - 1) + 3(x - 1)(x + 1) = ....)
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
MABYA
- Membre Relatif
- Messages: 401
- Enregistré le: 13 Mar 2015, 14:37
-
 par MABYA » 30 Mar 2015, 15:15
par MABYA » 30 Mar 2015, 15:15
que ce soit la méthode classique de @Willy (qui implique une division de polynôme par (x-1) ou l'astuce de @Zygomatique on arrive à (x-1)(x²+x+4), il faut se contenter de ça car x²+x+4 n'a pas de racines, à moins qu'il y ait une autre solution ?
-
mathelot
 par mathelot » 30 Mar 2015, 16:22
par mathelot » 30 Mar 2015, 16:22
MABYA a écrit:que ce soit la méthode classique de @Willy (qui implique une division de polynôme par (x-1) ou l'astuce de @Zygomatique on arrive à (x-1)(x²+x+4), il faut se contenter de ça car x²+x+4 n'a pas de racines, à moins qu'il y ait une autre solution ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
