bonjour !
j'arrive à la fin de mon exo mais voila je bloque :
j'ai demontré que a ( au carré) + b ( au carré )=4 et a*b = -1 pour
a=racine cubique de (2+ racine de 5)
b=racine cubique de (2- racine de 5)
ensuite j'ai demontré que pourtous nombres A et B que
(A (au cube )+B( au cube))= (A+B)(A²-AB+B²)
(A(au cube)+B(au cube))=(A+B)((A+B)²-3AB)
je dois en deduire que le réel a+b est solution de l'équation x(au cube )+3x-4=0
Alors voila deja ce que j'ai fait :
x(au cube)-3x-4=0
(a+b)(au cube) +3(a+b)-4=0
(a+b)((a+b)²-3ab)+3(a+b)-4=0
et voila je bloque là et je ne sais pas si mon raisonnement est bon ... :mur:
donc une petite aide serai sympa
merci d'avance tchou ! :help:
1ere S probleme de deduction
2 messages
- Page 1 sur 1
Bonsoir
MERCI d'avoir déjà fait quelquechose, de le montrer et d'indiquer précisément où tu bloques. :++:
Alors on va continuer à partir de là :
^3+3(a+b)-4)
[(a+b)^2+3]-4)
Puis, en me servant des relations démontrées antérieurement,
je chercherais à faire apparaître des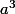 et des
et des 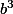
de manière à simplifier les calculs avec les racines cubiques
[(a+b)^2-3ab]-4) car
car 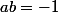 et donc aussi
et donc aussi 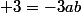
 en raison de l'une des deux égalités
en raison de l'une des deux égalités  établies précédemment
établies précédemment
 + (2-\sqr{5}) - 4)
Et là je te laisse terminer et conclure...
Une remarque encore : pour des valeurs de a et de b s'exprimant en racines cubiques,
le résultat suivant est surprenant.
MERCI d'avoir déjà fait quelquechose, de le montrer et d'indiquer précisément où tu bloques. :++:
Alors on va continuer à partir de là :
Jusque là c'est bon, c'est la ligne suivante qui ne me semble pas correcte :boubou88 a écrit:Alors voila deja ce que j'ai fait :
x(au cube)-3x-4=0
(a+b)(au cube) +3(a+b)-4=0
Moi je verrais plutôt ceci :(a+b)((a+b)²-3ab)+3(a+b)-4=0
Puis, en me servant des relations démontrées antérieurement,
je chercherais à faire apparaître des
de manière à simplifier les calculs avec les racines cubiques
Et là je te laisse terminer et conclure...
Une remarque encore : pour des valeurs de a et de b s'exprimant en racines cubiques,
le résultat suivant est surprenant.
j'ai demontré que a ( au carré) + b ( au carré )=4
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
