Le rectangle d'or maudit
55 messages
- Page 2 sur 3 - 1, 2, 3
(Relis mon message ci-dessus, j'ai ajouté des trucs.)
Pour l'égalité proposée, je parlais de la 4) : tu dois juste vérifier que x²-x-1 = la grosse formule. Pour ça tu pars de la droite, tu développes, et tu vérifies que ça redonne bien la quantité de gauche. (Ah oui, ne pas oublier : quand on demande de démontrer une égalité du type A = B, très souvent il est beaucoup plus simple de partir de B et de retomber sur A, plutôt que de partir de A et de retomber sur B.)
Pour l'égalité proposée, je parlais de la 4) : tu dois juste vérifier que x²-x-1 = la grosse formule. Pour ça tu pars de la droite, tu développes, et tu vérifies que ça redonne bien la quantité de gauche. (Ah oui, ne pas oublier : quand on demande de démontrer une égalité du type A = B, très souvent il est beaucoup plus simple de partir de B et de retomber sur A, plutôt que de partir de A et de retomber sur B.)
Robic a écrit:Shew : il ne s'agit pas de résoudre un trinôme du second degré, puisque dans la question 4) on demande de vérifier la factorisation directement.
Je crois que le plus difficile est le passage deà
Doki.light : c'est bon pour la question 3 ? Dans ce cas le plus dur est fait : en 4), tu as juste à vérifier l'égalité proposée, et en 5) tu utilises la calculatrice. (Si tu n'arrives pas à obtenir la propriété x²=x+1, dis-nous où tu en es.)
----
Apparemment tu n'as pas fini le 3)... Je te fais le début (que tu as déjà fait), puis des indications pour la fin. On part de :. Ensuite on divise par
pour le "faire passer à gauche" (façon de parler) :
.
Ensuite, grosse astuce :
L'idée est qu'on veut faire apparaître des. Là il reste à développer, tu verras que ça en fait apparaître un autre.
Je vois pas ou est le problème : on pose
Il n'y a pas de problème, c'est juste que c'est probablement la partie la plus difficile (il faut aller dans le bon sens). J'ai simplifié, et tout ça avait déjà été indiqué par Chan79. Du coup je ne sais pas trop où en est Doki.light.
Oui mais silteplease, dis-nous où tu en es...
silvousplease de repondre vite
Oui mais silteplease, dis-nous où tu en es...
Mais tu en es oùùùùùùùùùùùùùùùùùùùùùùùùùùùùùùùù ? :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur: :mur:
Est-ce que tu as trouvé=l^2) ?
?
Est-ce que tu as trouvé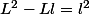 ?
?
Est-ce que tu as trouvé ?
?
Est-ce que tu as trouvé^2-\frac{L}{l}=1) ?
?
Est-ce que tu es allé plus loin ? Et si oui où en es-tu ?
Est-ce que tu as trouvé
Est-ce que tu as trouvé
Est-ce que tu as trouvé
Est-ce que tu as trouvé
Est-ce que tu es allé plus loin ? Et si oui où en es-tu ?
Le membre de droite !!!!!
On demande de démontrer que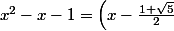 \left(x - \frac{1 - \sqrt{5}}{2} \right))
C'est lequel le membre de droite ? C'est celui qui est à droite du signe égal. Donc c'est...
Non, ce n'est pas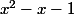 , il est à gauche du signe égal. Donc c'est...
, il est à gauche du signe égal. Donc c'est...
Et tu développes.
Le but est d'obtenir le membre de gauche, ce qui prouvera que le membre de droite est en effet égal au membre de gauche.
On demande de démontrer que
C'est lequel le membre de droite ? C'est celui qui est à droite du signe égal. Donc c'est...
Non, ce n'est pas
Et tu développes.
Le but est d'obtenir le membre de gauche, ce qui prouvera que le membre de droite est en effet égal au membre de gauche.
55 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
