Règle de l'hôpital
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 22 Sep 2006, 16:05
par euclide » 22 Sep 2006, 16:05
Bonjour, voilà un exemple de calcul de limite que l'on obtient facilement avec la règle de l'hôpital :
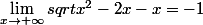
car on peut écrire :
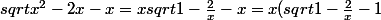= \frac{sqrt{1-\frac{2}{x}} - 1}{\frac{1}{x}}\,)
et :
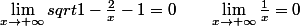
ainsi que :
\prime = \frac{1}{x^2 sqrt{\frac{x-2}{x}}} \qquad (\frac{1}{x})\prime = \frac{-1}{x^2})
et

donc :
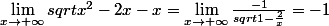
Seulement voilà pour la limite en -

je trouve les même formules et donc la même limite -1 avec cette méthode or je sais que c'est faux car la limite en -

est évidement +

(avec la méthode classique). Je sais que la règle de l'hôpital peut amener à des erreurs donc je compte sur vous pour me dire si mon raisonnement est juste ou non et pourquoi cette méthode ne fonctionne pas pour calculer cette limite en -

.
-
mirabobo
- Messages: 6
- Enregistré le: 22 Sep 2006, 12:42
-
 par mirabobo » 22 Sep 2006, 16:09
par mirabobo » 22 Sep 2006, 16:09
**********************
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Sep 2006, 16:14
par tize » 22 Sep 2006, 16:14
Si si, on peut appliquer la règle de l'Hôpital en

, voir
ici par exemple ...
-
mirabobo
- Messages: 6
- Enregistré le: 22 Sep 2006, 12:42
-
 par mirabobo » 22 Sep 2006, 16:24
par mirabobo » 22 Sep 2006, 16:24
**********************
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 22 Sep 2006, 16:35
par Alpha » 22 Sep 2006, 16:35
Personnellement je ne connais la règle de l'hôpital qu'en un certain

, et pas en + l'infini.
La règle de l'hôpital est juste la simple constatation que si

et

sont dérivables en

, la limite de
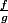
en

est le quotient des dérivées de

et de

en

(il suffit de l'écrire pour le voir).
Par conséquent, la démonstration même faisant intervenir la dérivée en un point, la règle de l'hôpital ne s'applique à ma connaissance qu'en un point

.
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 22 Sep 2006, 16:39
par Alpha » 22 Sep 2006, 16:39
J'ai oublié de préciser qu'il fallait que
=g(x_0)=0)
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Sep 2006, 16:39
par tize » 22 Sep 2006, 16:39
La règle de l'Hopital marche aussi en

! cf par exemple l'excellent Arnaudies Tome 2
Je pense qu'il y a un problème en

parce que quand euclide sort le

de la racine carré on a normalement

et non pas

...il y a donc une erreur dans ce que Euclide à écrit...
-
Alpha
- Membre Complexe
- Messages: 2176
- Enregistré le: 21 Mai 2005, 11:00
-
 par Alpha » 22 Sep 2006, 16:45
par Alpha » 22 Sep 2006, 16:45
Mais apparemment le lien envoyé par tize apporte une généralisation de cette règle. Si c'est le cas pour + et - l'infini, alors ça veut peut-être dire que la démonstration de cette généralisation dépassant le cadre du programme dans lequel ton livre se place, tu n'as pas le droit d'utiliser cette généralisation.
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 22 Sep 2006, 17:55
par euclide » 22 Sep 2006, 17:55
Et quel propriété l'expression

a pour que je ne puisse pas utiliser cette généralisation ?
-
Mikou
- Membre Rationnel
- Messages: 910
- Enregistré le: 06 Nov 2005, 13:17
-
 par Mikou » 22 Sep 2006, 18:09
par Mikou » 22 Sep 2006, 18:09
sisi en + infini la regle marche aussi, la preuve est plus complique et ne fut trouver que plus tard il me semble.
Sinon ici mutliplie par la quantite conjugé, sortir le x² ne sert a rien :)
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 22 Sep 2006, 18:22
par euclide » 22 Sep 2006, 18:22
Je suis d'acord mais ma question c'est "pourquoi la règle de l'hôpital ne marche pas en -

pour cette limite".
Et en réponse à "tize" en utilisant

en sortant x² je trouve cette expression :

ce qui revient au même...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Sep 2006, 18:33
par tize » 22 Sep 2006, 18:33
oui c'est vrai...j'avais remarqué...j'y réfléchi...
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Sep 2006, 18:39
par tize » 22 Sep 2006, 18:39
ça y est j'y suis...enfin je crois...
Pour pouvoir appliquer la règle de l'Hopital, il faut que la fonction au numérateur (et celle du dénominateur aussi...) tend vers 0 en

mais en corrigant ton erreur on trouve au numérateur :

qui ne tend pas vers 0 en

voilà pourquoi ca ne marche pas : parce que toutes les hypothèses ne sont pas vérifiées
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 22 Sep 2006, 20:09
par euclide » 22 Sep 2006, 20:09
Attend moi je trouve x(-

) et -

s'annule...
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 22 Sep 2006, 20:15
par euclide » 22 Sep 2006, 20:15
Autant pour moi, j'ai fais une erreur de signe t'as raison. Bravo
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Sep 2006, 20:54
par tize » 22 Sep 2006, 20:54
au "temps" pour moi :lol4:
-
oss007
- Membre Naturel
- Messages: 42
- Enregistré le: 16 Sep 2006, 09:39
-
 par oss007 » 22 Sep 2006, 21:48
par oss007 » 22 Sep 2006, 21:48
bonsoir
pourquoi ne multiplies-tu pas par l'expression conjuguée:
 + x)
, les numérateur et dénominateur ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 22 Sep 2006, 21:56
par tize » 22 Sep 2006, 21:56
Bonsoir,
lis tous les postes... on sait très bien qu'on peut fair cela mais la question etait ici de savoir si l'on pouvait ou non appliquer la règle de M. l'Hôpital...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités