Propriété primitive

[novicemaths]

Bonjour

Pourriez vous me donner la méthode pour trouver une primitive d'une fonction de la forme ci-dessous.



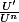
Merci.

A +

[mathelot]

bjr,
vous avez bien écrit "la méthode" :doh:



sachant que la dérivation décrémente l'exposant (n --> n-1), l'intégration incrémente l'exposant
(n ---> n+1).
nous cherchons donc la primitive sous la forme
En dérivant cette dernière expression, on trouve d'où

[novicemaths]

Re bonjour

Prenons un exemple que j'ai trouvé.



On commence par: u(x)=x²+2 et u'(x)=2x+4

Puis f(x)=*

Pourquoi ajouter

Avant de mettre la suite, j'attend votre réponse.

Mon souci est que je ne comprends pas le résonnement.

A +

[zzoe]

Bonjour,
u(x)=x²+2 et u'(x)=2x+4
ok, mais le numérateur est n(x)=x+2.
Or, il faut avoir 2x+4
on écrit donc que n(x)=(1/2)*(2x+4)
f(x) est alors de la forme 1/2*u'(x)/u(x)^3.
Il reste à appliquer la formule (à connaitre) citée par mathelot.

(ps "raisonnement" pas "résonnement" sinon, cela fait trop de bruit :lol3: )