Géo. Euclidienne

[mounch1810]

Bonjour,

Je me retrouve face à un problème simple en apparence, mais...

Soit u un vecteur unitaire de (E,N) euclidien. On pose P: E E tel que .
Il faut montrer que p est une projection orthogonale et trouver ses valeurs propres.

J'ai essayé de calculer mais je n’aboutis nul part.

Quelqu'un serait il faire?

Merci

[mathelot]

Bonjour,

Je me retrouve face à un problème simple en apparence, mais...

Soit u un vecteur unitaire de (E,N) euclidien. On pose P: E E tel que .
Il faut montrer que p est une projection orthogonale et trouver ses valeurs propres.

J'ai essayé de calculer mais je n’aboutis nulle part.

Quelqu'un saurait il faire?

Merci

on a déjà
donc
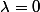
est linéaire ainsi que

on pourra discuter pour savoir si

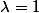
sais tu ce qu'est un hyperplan ? un orthogonal d'un sous espace ?

[mathelot]

p(x)=x équivaut à

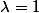
donc est valeur propre, le sous espace propre est de dimension dim(E)-1
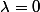
est valeur propre, le sous espace propre est de dimension 1

[mounch1810]

p(x)=x équivaut à

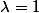
donc est valeur propre, le sous espace propre est de dimension dim(E)-1
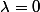
est valeur propre, le sous espace propre est de dimension 1

Merci de ton aide.