Bonjour à tous, :happy3:
Pourriez vous m'expliquer svp la chose suivante ? :
Définition : On dit qu'un polynôme

est résoluble par des radicaux si, et seulement si, les racines de

dans un corps des racines peuvent être construites à partir des coefficients de

en un nombre fini d'étapes faisant intervenir les quatre opérations élémentaires

,

,

,

et l'extraction de racines

pour des entiers naturels appropriés

. (
J'ai compris ce premier paragraphe. :happy3: )
Par contre, je comprends pas bien le paragraphe suivant, et son lien avec le premier paragraphe, le voici :
Il découle de cette définition, qu'un polynôme

est résoluble par des radicaux si, et seulement si, il existe des corps

tels que
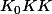
, le polynôme

est scindé dans

et pour tout entier

entre

et

, le corps

est obtenu à partir du corps

, par l'adjonction d'un élément

qui vérifie

pour un certain entiers positif

. En plus, nous pouvons supposer les

premiers car si
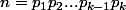
, où les

sont premiers, et si

est une racine

de

, on adjoint

en adjoignant successivement
 ^{p_{2} },...,\left( \left( \left( \alpha^{p_{1}}\right) \right) ...\right) ^{p_{k}}=\alpha $)
.
Merci d'avance pour vos éclaircissements. :happy3:
Edit : Ce paragraphe se trouve ici :
http://www.les-mathematiques.net/b/b/i/node3.php .
