Maths calcul intégrale par changement variable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
z^42
- Membre Naturel
- Messages: 60
- Enregistré le: 21 Sep 2014, 14:18
-
 par z^42 » 04 Mar 2015, 16:22
par z^42 » 04 Mar 2015, 16:22
Bonjour tout le monde
Je n'ai pas compris juste une étape de cette solution

((e)^(1/t))/t^2
u= 1/t= t^-1
du=1/t^2 dt
-du=1/t^2 dt
=;) e^(u).(-du) (pourquoi on n'écrit sous cette forme "e^(u)" alors que c'est ((e)^(1/t))/t^2, j'ai été revoir la définition mais je n'ai pas compris)
=-;)e^(u).(du)
=-e^(u) + C
=-e^(1/t)+C
merci d'avance bonne journée
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Mar 2015, 16:37
par Carpate » 04 Mar 2015, 16:37
z^42 a écrit:Bonjour tout le monde
Je n'ai pas compris juste une étape de cette solution

((e)^(1/t))/t^2
u= 1/t= t^-1
du=1/t^2 dt
-du=1/t^2 dt
=;) e^(u).(-du) (pourquoi on n'écrit sous cette forme "e^(u)" alors que c'est ((e)^(1/t))/t^2, j'ai été revoir la définition mais je n'ai pas compris)
=-;)e^(u).(du)
=-e^(u) + C
=-e^(1/t)+C
merci d'avance bonne journée
En ré-écrivant proprement :

Changement de variable :



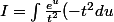=-\int e^{u}du = -e^u=-e^{\frac{1}{t}}+C)
-
z^42
- Membre Naturel
- Messages: 60
- Enregistré le: 21 Sep 2014, 14:18
-
 par z^42 » 04 Mar 2015, 16:53
par z^42 » 04 Mar 2015, 16:53
merci pour votre réponse
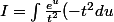=-\int e^{u}du)
Vous avez sortie le - et vous avez barrer les
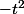
?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 04 Mar 2015, 17:57
par zygomatique » 04 Mar 2015, 17:57
salut
écrire
' = u'e^u)
ou
' = e^udu)
c'est la même chose si l'on sait que écrire

c'est écrire
)
c'est pourquoi il est toujours préférable d'écrire la variable ... pour savoir de quoi l'on parle et ce que l'on fait ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
