Décomposition en éléments

[Harmonie]

Bonjour, je dois donner la DES de

Soit , deg(A)=2
Soit , deg(B)=6
deg(A)<deg(B) donc E=0

le dénominateur est déjà factorisé et on a -1,0 et 1 racines doubles.

Je cherche donc F de la forme avec a,b,c,d,e,f des réels.
Seulement au moment de calculer les coefficients, j'ai déjà un problème..
Pour calculer a : a= (X-1)*F(X) |X=1 mais comment est-ce que je peux me débrouiller, en faisant ça, je trouve un dénominateur nul..
Faut-il que je commence plutôt par calculer et qu'ensuite je dérive pour trouver a ?

Ou alors, est-ce qu'il faut écrire , là, je peux calculer a, b et c. Mais pour d e f ? J

Merci d'avance

[mathelot]

pourquoi on ne pose pas ?
:doh:

[zygomatique]

salut




on multiplie par et on pose x = 1 ==> on obtient b

on multiplie par et on pose x = -1 ==> on obtient f

on multiplie par et on pose x = 0 ==> on obtient d


ensuite on peut remarquer que :



or



donc c = 0 et a = -e .... (et f = b)

en évaluant en 2 par exemple on en déduit a ....

:lol3:

[Harmonie]

pourquoi on ne pose pas ?
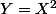
:doh:

Parce que je n'en ai pas eu l'idée, et aussi parce qu'on a pas utilisé de changement de variables pour trouver des décompositions en éléments simples..
Si développe le carré sur B(X)
B(X)= (X-1)²*X²*(X+1)² = (X² + 1 - 2X) * X² * (X² + 1 + 2X)
B(X)= Y^3 - 2Y² + Y

Du coup, je peux étudier 3Y^2-1 / Y^3 - 2Y² + Y = 3Y^2-1 / Y(Y-1)(Y+1)
Il n'ya toujours pas de partie entière, les racines sont toujours -1,0 et 1
Et du coup je cherche F= a/Y + b/(Y-1) + c/(Y+1)
Je trouve a=b=c=1 ce qui me semble bizarre.. j'ai utilisé la méthode a=Y*F(Y)|Y=0 que j'ai réitérée pour b et c.

Sans poser Y=X², Enfait, il faudrait que je commence par calculer f,
pour calculer e j'utiilise la dérivée de 1/X²
pour calculer d j'utilise X²*F(X)|X=0
pour calculer c j'utilise la dérivée de 1/(X-1)² ?
pour calculer b j'utilise (X-1)²*F(X)|X=1
et pour calculer a, j'utilise une valeur que je choisis ?

[Harmonie]

J'ai mis trop de temps à envoyer ma réponse, je n'avais pas vue la tienne Zygomatique, tu conforte alors ma dernière idée, enfin ce que tu dis est plus clair et plus juste.
J'avais un brouillon ou j'utilisais la parité de F, mais je ne sais par quel miracle, j'ai décidé que B(X) n'avait pas de racines réelle et donc qu'au numérateur on avait des polynomes du premier degré..

Une autre question, qui rejoint mon post du dessus du coup, je choisis vraiment ce que je veux pour a ?

[zygomatique]

si cette décomposition est vraie pour tous les réels de l'ensemble de définition de F alors elle vraie pour ceux que je veux ...

je chosis donc "le plus simple" pour déterminer ma dernière inconnue ....

[Harmonie]

D'accord, merci :)