bonjour je travaille en ce moment sur les cercles trigonométriques, et je dois trouver la valeur d'un cosinus et d'un sinus de x, à partir de ma calculatrice, x appartenant à une intervalle.
mais x n'appartient pas à l'intervalle et ma prof a dit que l'on apprendra à changer la valeur de x pour qu'il appartienne à l'intervalle.
Mais j'aimerais savoir si vous savez comment faire ?
merci d'avance !
TRIGONOMETRIE (seconde)
11 messages
- Page 1 sur 1
oui, le cercle trigo est divisé en quatre quadrants et tout se passe modulo 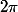
par exemple

on divise 53 par 8

on soustraie

- on commence par réduire l'argument pour qu'il appartienne à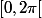
ou à je sais jamais.
je sais jamais.
 établit une relation entre le quadrant 3 et le quadrant 1
établit une relation entre le quadrant 3 et le quadrant 1
(points opposés par un diamètre)
 établit une relation entre le quadrant 4 et le quadrant 1
établit une relation entre le quadrant 4 et le quadrant 1
(points symétriques par rapport à x'Ox)
 établit une relation entre le quadrant 2 et le quadrant 1
établit une relation entre le quadrant 2 et le quadrant 1
(points symétriques par rapport à y'Oy)
On peut raffiner..
 permute à l'intérieur du 1er quadrant par rapport à la 1ere bissectrice d'équation Y=X
permute à l'intérieur du 1er quadrant par rapport à la 1ere bissectrice d'équation Y=X
par exemple
on divise 53 par 8
on soustraie
- on commence par réduire l'argument pour qu'il appartienne à
ou à
(points opposés par un diamètre)
(points symétriques par rapport à x'Ox)
(points symétriques par rapport à y'Oy)
On peut raffiner..

un petit dessin pour illustrer le modulo
en vert l'angle de 180° (= pi radians)
en rouge l'angle de 540° = 180° + 360° (= 3 * pi radians)
les 2 angles sont confondus sur le cercle trigo
ils ont donc le même cosinus et le même sinus
si tu as un angle x en dehors de 0 à 360° (=0 à 2 * pi radians), tu peux lui ajouter ou enlever 360°, qui correspond à un tour complet, autant de fois que tu veux, tu obtiendras le même cosinus et le même sinus
avec x en degrés :
cos (x + k * 360°) = cos (x)
ou avec x en radians :
cos (x + 2 * k * pi) = cos (x)
Trigo
Mais enfaite je ne cherche pas le cosinus d'un Angle mais d'un nombre assimilé au coordonnées dun point sur le cercle ;( et je ne comprends pas
c'est pareil
un point sur le cercle correspond à un angle et réciproquement
par ex sur le dessin plus haut, le point I correspond à un angle de 0° (=0 radians)
le point J correspond à un angle de 90° (=pi/2 radians)
le point M correspond à un angle de 180° (=pi radians)
quand tu écris cos(x), x est un nombre qui donne la valeur d'un angle
x est exprimé en degrés, en radians, en grades ...

image trouvée sur http://homeomath2.imingo.net/cosinus.htm
sinon donne nous le nombre (ou point) dont tu cherches le cosinus, ce sera peut etre plus facile d'expliquer
un point sur le cercle correspond à un angle et réciproquement
par ex sur le dessin plus haut, le point I correspond à un angle de 0° (=0 radians)
le point J correspond à un angle de 90° (=pi/2 radians)
le point M correspond à un angle de 180° (=pi radians)
quand tu écris cos(x), x est un nombre qui donne la valeur d'un angle
x est exprimé en degrés, en radians, en grades ...

image trouvée sur http://homeomath2.imingo.net/cosinus.htm
sinon donne nous le nombre (ou point) dont tu cherches le cosinus, ce sera peut etre plus facile d'expliquer
il y a , comme tu le constates, une application d'enroulement,
d'ensemble de définition les réels et pour ensemble d'arrivée le cercle trigo U:

)
cette application est périodique,ie,
périodique,ie, =M)
Maintenant , un point du cercle possède deux coordonnées cartésiennes (X,Y)
l'application "e" définit donc deux fonctions réelles qui sont les coordonnées de M, point du cercle,
dans le repère cartésien (O,I,J)
;sin(x)))
par exemple, le point à coordonnées positives situé sur le cercle à l'intersection avec la 1ère bissectrice du repère , droite d'équation Y=X vérifie

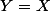



)
d'ensemble de définition les réels et pour ensemble d'arrivée le cercle trigo U:
cette application est
Maintenant , un point du cercle possède deux coordonnées cartésiennes (X,Y)
l'application "e" définit donc deux fonctions réelles qui sont les coordonnées de M, point du cercle,
dans le repère cartésien (O,I,J)
par exemple, le point à coordonnées positives situé sur le cercle à l'intersection avec la 1ère bissectrice du repère , droite d'équation Y=X vérifie
trigo
Merci beaucoup de votre aide, cependant je n'arrives pas à visualiser donc je vais vous donner mon fameux point : x=1,6 et doit appartenir à [-pi ; 0], et son cosinus est égal à 0,4.
Comment puis-je faire ?
Comment puis-je faire ?
ariana1207 a écrit:Merci beaucoup de votre aide, cependant je n'arrives pas à visualiser donc je vais vous donner mon fameux point : x=1,6 et doit appartenir à [-pi ; 0], et son cosinus est égal à 0,4.
Comment puis-je faire ?
déjà, ton énoncé est erroné.
a) soit x=1.6 est en degré et son cosinus vaut quasiment 1;
b) soit x=1.6 est en radian et son cosinus vaut -0.292
dans le cas (b),
de toutes façons, on place les points en "remontant" l'abscisse cartésienne X=-0.292
lue sur x'Ox , sur le cercle en un point d'ordonnée Y négative Y=-0.956
grosso modo, si (I=est,J=nord,K=ouest,L=sud) sont les quatre points cardinaux, le point cherché est légèrement à gauche de L.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
