Marche aléatoire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
 par Charmander » 26 Fév 2015, 15:06
par Charmander » 26 Fév 2015, 15:06
Bonjour,
On considère une marche aléatoire sur Z,
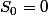
et
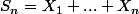
où les
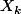
sont des variables aléatoires de Bernouilli prenant la valeur 1 avec une probabilité 0.5 et la valeur -1 sinon.
Le temps d'attente du premier retour à l'origine est noté
)
On note
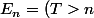)
Montrer que
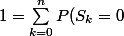P(E_{n-k}))
Le n-k me perturbe un peu... Pourquoi n-k ? Surtout qu'il me semble que pour certaines valeurs de k les évènements
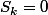
et

sont incompatibles.
A priori c'est une formule de probabilité totale mais je ne vois pas quelle probabilité égal à un il faut décomposer. Y aurait-il une erreur dans l'énoncé ?
Merci d'avance.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 26 Fév 2015, 17:32
par zygomatique » 26 Fév 2015, 17:32
salut
je comprends déjà même pas pourquoi la somme serait finie .....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
 par Charmander » 26 Fév 2015, 17:54
par Charmander » 26 Fév 2015, 17:54
Je pense que c'est dû au fait que la probabilité qu'on doit trouver est celle d'un évènement lié à l'état de la n-ième itération avec le n fixé (est-on à l'origine ? Combien de retour à l'origine ? etc)...
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 26 Fév 2015, 17:55
par Doraki » 26 Fév 2015, 17:55
Certes, E_{n-k} n'est pas indépendant avec Sk (et même ils sont souvent incompatible),
mais P(E_{n-k}) c'est juste un nombre, et c'est la probabilité que, en partant de 0, on ne revient pas sur 0 dans les n-k premiers pas.
Maintenant si tu regardes P(Sk=0)P(E_{n-k}) ça pourrait décrire la probabilité de quel événement (en fonction de k et de n) ?
-
Charmander
- Membre Naturel
- Messages: 90
- Enregistré le: 13 Oct 2013, 16:22
-
 par Charmander » 26 Fév 2015, 18:11
par Charmander » 26 Fév 2015, 18:11
C'est la probabilité qu'on ne revienne pas avant n-k multipliée par la probabilité qu'on soit à l'origine à l'instant k... Mais ça peut pas être la probabilité de l'intersection de ces deux évènements puisqu'ils sont incompatibles... :triste: :triste:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 27 Fév 2015, 14:12
par Doraki » 27 Fév 2015, 14:12
C'est quoi la probabilité, en sachant/supposant que Sk=0, de ne pas revenir sur 0 dans S(k+1), S(k+2),..., Sn ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
