Fonction à plusieurs variables
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 25 Fév 2015, 12:09
par mamas67 » 25 Fév 2015, 12:09
Bonjour
on a g(x1,x2,... ,xr) = somme pour i allant de 1 jusqu'a r des (1-xi)^n
avec 0
On me demande de trouver les points critiques de g sous la contrainte x1+ .. + xr = 1
Les dérivées partielles H d'odre 1 de g sont :
Hi(g)(x1, ... , xr) = -n(1-xi)^(n-1)
Mais après je vois pas comment continuer ...
Qqu pourrait m'aider svp ?
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 25 Fév 2015, 17:31
par BiancoAngelo » 25 Fév 2015, 17:31
mamas67 a écrit:Bonjour,
on a g(x1,x2,... ,xr) = somme pour i allant de 1 jusqu'a r des (1-xi)^n
avec 0<xi<1
On me demande de trouver les points critiques de g sous la contrainte x1+ .. + xr = 1
Les dérivées partielles H d'odre 1 de g sont :
Hi(g)(x1, ... , xr) = -n(1-xi)^(n-1)
Mais après je vois pas comment continuer ...
Qqu pourrait m'aider svp ?
Salut, on a donc :
 = \sum\limits_{i=0}^{r} (1-x_i)^n)
et
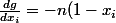^{n-1})
Ce qui signifie que
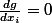
seulement pour
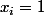
ce qui est impossible d'après les hypothèses.
Donc aucun point critique.
Etrange, vu qu'ils donnent en plus une condition sur les

:ptdr:
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 25 Fév 2015, 17:33
par BiancoAngelo » 25 Fév 2015, 17:33
Néanmoins, il n'y a pas de conditions sur le n.
Es-tu sûr qu'il soit supérieur ou égal à 1 ?
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 25 Fév 2015, 17:42
par mamas67 » 25 Fév 2015, 17:42
Ouais, c'est aussi ce que j'avais trouvé, mais le résultat me paraissait spécial .. Enfin bon =)
Juste encore après, on me demande d'étudiele signe de la forme quadratique qB associé a la matice hessienne de g en tout point de ]O,1[^r
On a Hi,j(g)(x1, ..., xn)
= 0 si i <>j
= n(n-1)(1-xi)^(n-2) > 0 si i=j ( car n>=2 par hypothèse)
Du coup la matrice hessienne de g, est diagonale et ses valeurs propres sont ses coef diagonaux, qui sont toutes stricement positives.
= > qB>0
J'aurais juste aimé savoir si mon raisonnement est juste =]
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 25 Fév 2015, 17:42
par SLA » 25 Fév 2015, 17:42
BiancoAngelo a écrit:Salut, on a donc :
 = \sum\limits_{i=0}^{r} (1-x_i)^n)
et
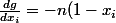^{n-1})
Ce qui signifie que
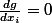
seulement pour
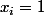
ce qui est impossible d'après les hypothèses.
Donc aucun point critique.
Etrange, vu qu'ils donnent en plus une condition sur les

:ptdr:
Angelo a du mal lire le problème. Il s'agit de minimiser ou maximiser

sur la partie

avec
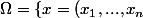 \in \mathbb{R}^n; 0<x_i<1 \})
et
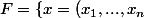 \in \mathbb{R}^n; h(x)=x_1+...+x_n=0\})
.
Or

n'est pas ouvert, donc le gradient de g aux points de minimisations/maximisation (s'il y en n'a) pas de raison de s'annuler.
En revanche, tu dois avoir un théorème qui te dit qu'il existe un réel

(appelé multiplicateur de Lagrange) tel que si
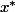
est un point maximise/minimise g alors
=\lambda dh(x^*))
ou encore
 = \lambda \partial_i h(x^*), \forall 1\leq i \leq n)
.
Ce genre de formule te dit quelque chose?
EDIT: ce n'est pas
=x_1+...+x_n)
mais
=x_1+...+x_n -1)
. Merci à BiancoAngelo
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 25 Fév 2015, 17:44
par mamas67 » 25 Fév 2015, 17:44
Oui effectivement, on a cette formuel dans le cours, mais après je vois pas trop comment l'utiliser ...
En fait, nous on la mise dans la partie "contrainte quelconque".
Or là, on a une contrainte d'égalité linéaire ...
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 25 Fév 2015, 17:53
par SLA » 25 Fév 2015, 17:53
mamas67 a écrit:Oui effectivement, on a cette formuel dans le cours, mais après je vois pas trop comment l'utiliser ...
J'imagine que c'est un exo d'application ^^.
On va supposer dans un premier temps l'existence d'un minimum/maximum (au besoin, je vois comment le prouver, mais ça me parait hors sujet).
On dispose des égalités
 = \lambda \partial_i h(x^*), \forall 1\leq i \leq n)
Or
)_j = -n(1-x_i)^{n-1} \delta_{i,j})
et
)_j= \delta_{i,j})
Ce qui impose que pour tout i ...
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 25 Fév 2015, 17:57
par mamas67 » 25 Fév 2015, 17:57
je vous avoue que je suis un peu perdu ... =]
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 25 Fév 2015, 17:59
par SLA » 25 Fév 2015, 17:59
mamas67 a écrit:je vous avoue que je suis un peu perdu ... =]
Alors, plus lentement. Qu'est ce qui te parle le plus: dérivée partielle, gradient ou différentielle?
Quel est l'énoncé du théorème que tu trouves dans ton cours?
Le reste ne sera que de l'écriture.
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 25 Fév 2015, 18:03
par mamas67 » 25 Fév 2015, 18:03
Perso, je suis plus à l'aise avec les dérivées partielles
Dans mon cours, j'ai :
Si f de classe C1 sur un ouvert, admet un extremeum local en A sous la contrainte non critique C d'quation phi(x)=c, alors il existe un réel lamba tq :
phi(A) = c
H(f)(A) = lambda*H(phi)(A) avec H le gradient
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 25 Fév 2015, 18:08
par SLA » 25 Fév 2015, 18:08
mamas67 a écrit:Perso, je suis plus à l'aise avec les dérivées partielles
Dans mon cours, j'ai :
Si f de classe C1 sur un ouvert, admet un extremeum local en A sous la contrainte non critique C d'quation phi(x)=c, alors il existe un réel lamba tq :
phi(A) = c
H(f)(A) = lambda*H(phi)(A) avec H le gradient
Très bien. Par contre je noterais le gradient de g:

.
Ici,
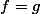
,
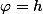
et
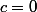
. il existe donc

réel tel que
= \lambda \nabla h(x^*))
.
Il te reste à calculer les matrices colonnes
)
et
)
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 25 Fév 2015, 18:11
par mamas67 » 25 Fév 2015, 18:11
Ah, ca y est =)
Je crois que j'ai compris =]
Vérifie tout ca et vous tiens au courant =)
Merci !
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 25 Fév 2015, 18:13
par BiancoAngelo » 25 Fév 2015, 18:13
SLA a écrit:Angelo a du mal lire le problème. Il s'agit de minimiser ou maximiser

sur la partie

avec
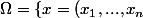 \in \mathbb{R}^n; 0<x_i<1 \})
et
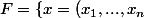 \in \mathbb{R}^n; h(x)=x_1+...+x_n=0\})
.
Or

n'est pas ouvert, donc le gradient de g aux points de minimisations/maximisation (s'il y en n'a) pas de raison de s'annuler.
En revanche, tu dois avoir un théorème qui te dit qu'il existe un réel

(appelé multiplicateur de Lagrange) tel que si
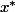
est un point maximise/minimise g alors
=\lambda dh(x^*))
ou encore
 = \lambda \partial_i h(x^*), \forall 1\leq i \leq n)
.
Ce genre de formule te dit quelque chose?
Ca oui c'est évident, je pensais qu'on parlait de la recherche des points où le gradient s'annulait... Au temps pour moi!
Sinon :
Tu es sûr que ce n'est pas plutôt :

avec
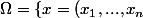 \in \mathbb{R}^n; 0<x_i<1 \})
et
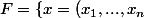 \in \mathbb{R}^n; h(x)=x_1+...+x_n=1\})
. ?
(le 1 de la fin)
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 25 Fév 2015, 18:14
par SLA » 25 Fév 2015, 18:14
BiancoAngelo a écrit:Ca oui c'est évident, je pensais qu'on parlait de la recherche des points où le gradient s'annulait... Au temps pour moi!
Sinon :
Tu es sûr que ce n'est pas plutôt :

avec
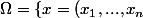 \in \mathbb{R}^n; 0<x_i<1 \})
et
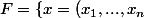 \in \mathbb{R}^n; h(x)=x_1+...+x_n=1\})
. ?
(le 1 de la fin)
Effectivement! merci pour la correction.
-
BiancoAngelo
- Membre Rationnel
- Messages: 585
- Enregistré le: 12 Déc 2011, 23:06
-
 par BiancoAngelo » 25 Fév 2015, 18:18
par BiancoAngelo » 25 Fév 2015, 18:18
mamas67 a écrit:Perso, je suis plus à l'aise avec les dérivées partielles
Dans mon cours, j'ai :
Si f de classe C1 sur un ouvert, admet un extremeum local en A sous la contrainte non critique C d'quation phi(x)=c, alors il existe un réel lamba tq :
phi(A) = c
H(f)(A) = lambda*H(phi)(A) avec H le gradient
Je ne connaissais pas ce théorème (en fait je découvre les problèmes d'optimisation de ce genre au fur et à mesure des posts des intervenants du forum).
Mais du coup, vu que c'est une implication, si on trouve un tel lambda, ça ne signifie pas qu'on a forcément un point critique, ou alors c'est équivalent ?
-
SLA
- Membre Relatif
- Messages: 335
- Enregistré le: 29 Déc 2012, 21:55
-
 par SLA » 25 Fév 2015, 18:23
par SLA » 25 Fév 2015, 18:23
BiancoAngelo a écrit:Je ne connaissais pas ce théorème (en fait je découvre les problèmes d'optimisation de ce genre au fur et à mesure des posts des intervenants du forum).
Mais du coup, vu que c'est une implication, si on trouve un tel lambda, ça ne signifie pas qu'on a forcément un point critique, ou alors c'est équivalent ?
Non, c'est en cas d'existence d'un extrema que la relation est vérifiée. De même que sur un ouvert, si une fonction admet un extremum alors sa dérivée (ou son gradient) s'y annule, la réciproque est fausse.
L'existence d'extrema est souvent obetnue par des arguments de compacité ou de suites minimisantes/maximisantes. Dans le cas où l'on obtient l'existence par compacité, la plupart du temps il faudrat chercher un autre théorème de maximisation sous contraintes (Karush-Kuhn-Tucker).
Le concepteur de l'exercice d'ici a pris soin d'éviter le problème ici.
-
mamas67
- Membre Naturel
- Messages: 46
- Enregistré le: 21 Oct 2014, 13:27
-
 par mamas67 » 28 Fév 2015, 12:44
par mamas67 » 28 Fév 2015, 12:44
mamas67 a écrit:Ouais, c'est aussi ce que j'avais trouvé, mais le résultat me paraissait spécial .. Enfin bon =)
Juste encore après, on me demande d'étudiele signe de la forme quadratique qB associé a la matice hessienne de g en tout point de ]O,1[^r
On a Hi,j(g)(x1, ..., xn)
= 0 si i j
= n(n-1)(1-xi)^(n-2) > 0 si i=j ( car n>=2 par hypothèse)
Du coup la matrice hessienne de g, est diagonale et ses valeurs propres sont ses coef diagonaux, qui sont toutes stricement positives.
= > qB>0
J'aurais juste aimé savoir si mon raisonnement est juste =]
C'est bon du coup ? =)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
