Suite bornee - 1ere S

[Combattant204]

Bonsoir tout le monde,
J'ai besoin d'aide dans cet exercice

Soit Un = (2n - 1)/(n + 1) pour tout n E N
1.Etudier le sens de variation de cette suite.
2.Montrer que pour tout n >= 0, -1 <= Un < 2.
3.A partir de quel entier n tous les termes de la suite sont-ils compris entre 1,5 et 2? Justifier.

Ma reponse

1. On calcule Un+1-Un et on compare le resultat a 0:
Soit (2n + 1)/(n + 2) - (2n - 1)/(n + 1)
= ((2n + 1)(n + 1) - (2n - 1)(n + 2))/((n + 2)(n + 1))
= ((2n^2 + 2n + n + 1 - (2n^2 + 4n - n - 2))/((n + 2)(n + 1))
= (2n^2 + 3n + 1 - 2n^2 - 4n + n + 2)/((n + 2)(n + 1))
=3/((n + 2)(n + 1))
Or 3 > 0 et pour tout n E N (n + 2)(n + 1) > 0 d'ou Un+1 - Un > 0.
Un est une suite croissante.

2.Pour montrer que -1 <= Un < 2
On procedera par manipulation d'inegalitees.
Montrer que Un >= - 1 revient a montrer que Un + 1 >= 0
On a donc Un + 1 = (2n - 1)/(n + 1) + 1
Or pour tout n E N 2n - 1 > 0 ;
Pour tout n E N (n + 1) > 0 et on a 1 > 0
C'est a dire que Un + 1 >= 0 or Un >= - 1
Montrer que Un <= 2 revient a montrer que Un - 2 <= 0
On a donc Un - 2 = (2n - 1)/(n + 1) - 2
= (2n - 1 - 2n - 2)/(n + 1)
= -3/(n + 1)
Or - 3 < 0 et n + 1 > 0
C'est a dure que Un - 2 < 0 or Un < 2

Ok dans la 3 je ne sais absolument rien faire.

J'aimerais surtout que vous verifiez si ce que j'ai fait est juste,de l'aide s'il vous plait. :help:

[Marc0]

c'est marrant la 3 me parait plus simple que les autres questions
1.5< (2n-1)/(n+1)
1.5n+1.5<2n-1
...

A partir de n = 5 Un est compris entre 1.5 et 2 (car tu as prouvé qu'elle était inférieure à 2 et qu'elle est croissante)
Essai pour n = 5
(5*2-1)/(5+1) = 9/2 = 1.5

[Waax22951]

Bonjour,
Notons que pour la deuxième question, il y a plus simple pour montrer que .
En effet, on a pour tout entier naturel n, par croissance de la suite :


Or on a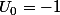 , soit encore pour tout entier naturel n:


Après ta façon de procéder est juste, mais on pourra souvent te demander ça pour des exos type bac, et c'est bien de penser à se servir de la croissance (ou de la décroissance) d'un suite pour gagner du temps..!

Sinon pour la question 3, en notant le premier rang de tel que , on a pour tout entier naturel n, toujours par croissance de la suite:


Soit . Ainsi, il te suffit juste de déterminer la valeur de :lol3:

Bonne soirée :lol3:

[Combattant204]

c'est marrant la 3 me parait plus simple que les autres questions
1.5< (2n-1)/(n+1)
1.5n+1.5<2n-1
...

A partir de n = 5 Un est compris entre 1.5 et 2 (car tu as prouvé qu'elle était inférieure à 2 et qu'elle est croissante)
Essai pour n = 5
(5*2-1)/(5+1) = 9/2 = 1.5

Merci beaucoups,j'ai bien compris! C'est vrai,cette question est incroyablement plus simple que les autres.

[Combattant204]

Bonjour,
Notons que pour la deuxième question, il y a plus simple pour montrer que .
En effet, on a pour tout entier naturel n, par croissance de la suite :


Or on a , soit encore pour tout entier naturel n:


Après ta façon de procéder est juste, mais on pourra souvent te demander ça pour des exos type bac, et c'est bien de penser à se servir de la croissance (ou de la décroissance) d'un suite pour gagner du temps..!

Sinon pour la question 3, en notant le premier rang de tel que , on a pour tout entier naturel n, toujours par croissance de la suite:


Soit . Ainsi, il te suffit juste de déterminer la valeur de :lol3:

Bonne soirée :lol3:

Merci de m'avoir montre le plus simple,j'ai 1 derniere question
pouviez vous me montrer aussi comment proceder de manier plus simple (a ce que j'ai fait) a montrer que Un < 2 pour tout n? Ca m'aidera vraiment.

[Waax22951]

Merci de m'avoir montre le plus simple,j'ai 1 derniere question
pouviez vous me montrer aussi comment proceder de manier plus simple (a ce que j'ai fait) a montrer que Un < 2 pour tout n? Ca m'aidera vraiment.

Je ne pense pas que l'on puisse faire plus simple que ce que tu as fait. On peut cependant raisonner par récurrence, mais je trouve ça plus long..!

Bonne journée !