Matrices

[pluie2]

Bonjour à tous, je ne parviens pas à faire la deuxième partie de cette nouvelle épreuve type de maths pour le concours agro-véto et aucun corrigé n'est disponible. Serait il possible que quelqu'un m'y aide :

https://www.concours-agro-veto.net/IMG/pdf_Epreuve_A_propagation_relu3.pdf


voici ce que j'ai écrit :
B.1.a) P(X_(n+1)=i/X_n=j)=0. En effet, on nous dit que chacun des i porteurs devient sain à l'instant n+1 donc il y a une proba 0 qu'il y en ait de porteurs de V.
La loi conditionnelle suit une loi hypergéométrique de paramètres (2,i,i/2) ?

je vois à peu près comment trouver M, j'ai fait un arbre de proba mais pour les i porteurs, on ne nous donne pas les probabilités, est ce p, 1-p ou alors i/2 ? j représente t-il la part de la population autre que i à savoir ceux sains?

b) P(X_(n+1)=i)=P(X_(n+1)=i/X_n=i)P(X_n=i)+P(X_(n+1)=i/X_n=j)P(X_n=j)
du coup ici:
P(X_n=0)=(1-p)
P(X_n=1)=1/2 * 1/2=1/4
P(X_n=2)=1/2

donc P(X_n+1=0)=(1-p)*(1-p); P(X_n+1=1)=p(1-p); P(X_n+1=2)=p(1-p)

mais ça ne correspond pas vraiment avec la matrice....

U_n=M^n*U_0

c) Pour montrer que ce sont les valeurs propres de M, on résout le système à partir de la matrice de M. ok pour les vecteurs propres

d) M est triangulaire, admet des valeurs propres et la dimension de ces vecteurs propres = 3 donc M est diagonalisable. ok pour le reste

e) ?

B2.
a) On sait que P=aX²+bX+c d'après l'énoncé. Je pense qu'il faut prendre au cas par cas, pour k=0 ,1 puis 2 et on regarde si on trouve l'égalité dans les 2 cas
b)

je suis bloquée ensuite
merci !!

[arnaud32]

B1a:
P(X(n+1)=0 | X(n)=0) ca veut dire qu'en n aucun individu n'est atteint et qu'aucun des deux n'est contamines en n+1 la proba est donc (1-p)*(1-p)
P(X(n+1)=1 | X(n)=0) ca veut dire qu'en n aucun individu n'est atteint et qu'un des deux est contamines en n+1 la proba est donc p*(1-p)+(p-1)*p=2*p(p-1)
P(X(n+1)=0 | X(n)=0) ca veut dire qu'en n aucun individu n'est atteint et que les deux sont contamines en n+1 la proba est donc p*p

etc ...

[arnaud32]

B1b

donc

[arnaud32]

B1c
tu peux utiliser le poynome carcteristique et rechercher les vecteurs propres en resolvant MX=l*X

B1d
il ya trois vecteurs propres distincts (car 3 valeurs propres distinctes puisque 0<p<1) qui forment donc une base de R^3 et la matrice est diagonalisable
la matrice de passage s'obtient avec les vecterus propres dasn la base d'origine

B1e
tu regardes se qui se passe pour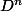 elle converge vers ...
et utilises les resultats pour prouver que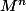 converge et donner sa limite

[arnaud32]

B2a

tu ecris la definition de Phi et tu factorises

B2b

tu utilises teas vecteurs propres de M

[arnaud32]

B3a

[pluie2]

re bonjour

Pour la partie B1 j'ai essayé de faire de mon côté et je retrouve les mêmes résultats et méthodes que vous m'avez proposé donc OK

Par contre pour la B2, je n'arrive pas dès la première question car je ne vois pas justement comment exploiter phi et sa définitino.

Dois je calculer phi(X^0), phi(X^1) et phi(X²) ? Si oui comment m'aider de la matrice M ?

B3.a) Je comprends votre expression mais en revanche je ne vois pas comment vous l'avez trouvée

du coup pour la suite avez vous une idée??