Dénombrement - Série entière

[Charmander]

Bonjour,

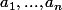
Soit des entiers naturels non nuls premiers entre eux dans leur ensemble. Pour n 1, on note le nombre de k-uplets tels que
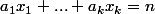
Déterminer un équivalent de , en considérant

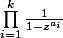
Comme l'exercice est posé dans un chapitre sur les séries entières, je suppose qu'il faut suivre la démarche classique qui est de trouver une relation de récurrence sur , la relier à la série entière de la fonction indiquée, identifier les coefficients et passer à l'équivalent. Mais je n'arrive pas à voir la relation de récurrence... En essayant sur des couples simples tels que (1,2) et les valeurs petites de n, je trouve des résultats qui semblent plus ou moins aléatoires et fortement dépendants des ... Est-il possible de trouver une relation de récurrence, voire expliciter u ? Merci.

[zygomatique]

salut



pour |z| < 1

....

[Charmander]

Je vois, merci !