Terminale - Complexe equation 2nd degré
15 messages
- Page 1 sur 1
Terminale - Complexe equation 2nd degré
Bonjour,
Je suis en Terminal STI et on ma donner pour devoir un DM. Cependant je bloque à la première question :mur: .
Voici l'énoncé :
On considère l'équation z²-4z+13 = 0 ou z est un nombre complexe.
Première question : Calculer sont discriminent. Cette équation à t'elle des solutions réelles ?
Alors j'ai calculer Delta à la main puis vérifier à la calculette avec cette formule :
b² - 4.a.c J'optiens : (-4z)² - (4 * (z)² * 13) ce qui me donne delta = 36.
Vu que delta est positif l'équation à deux solutions réels et pas de solutions complexes, non ?
Seulement les questions suivantes sont :
Vérifier pour tout nombre complexe z : z² - 4z + 13 = (z - 2 + 3i)(z - 2 - 3i)
En déduire que l'équation proposée à deux solutions complexes conjuguées que l'on déterminera.
J'en déduit que à la première question j'aurais du trouvé un Delta négatif non ?
Merci de votre aide :)
Je suis en Terminal STI et on ma donner pour devoir un DM. Cependant je bloque à la première question :mur: .
Voici l'énoncé :
On considère l'équation z²-4z+13 = 0 ou z est un nombre complexe.
Première question : Calculer sont discriminent. Cette équation à t'elle des solutions réelles ?
Alors j'ai calculer Delta à la main puis vérifier à la calculette avec cette formule :
b² - 4.a.c J'optiens : (-4z)² - (4 * (z)² * 13) ce qui me donne delta = 36.
Vu que delta est positif l'équation à deux solutions réels et pas de solutions complexes, non ?
Seulement les questions suivantes sont :
Vérifier pour tout nombre complexe z : z² - 4z + 13 = (z - 2 + 3i)(z - 2 - 3i)
En déduire que l'équation proposée à deux solutions complexes conjuguées que l'on déterminera.
J'en déduit que à la première question j'aurais du trouvé un Delta négatif non ?
Merci de votre aide :)
Dire que -36 = (6i)² est utile pour trouver les racines complexes par la méthode générale, mais celle-ci n'est pas au programme du lycée, donc ne l'utilise pas, dis juste que Delta = -36.
En général, on cherche les racines complexes et on en déduit la factorisation. Mais comme la recherche des racines complexes n'est pas au programme, ici on te donne la factorisation (la question suivante) et tu dois en déduire les racines complexes. Cette fois c'est faisable en terminale.
En général, on cherche les racines complexes et on en déduit la factorisation. Mais comme la recherche des racines complexes n'est pas au programme, ici on te donne la factorisation (la question suivante) et tu dois en déduire les racines complexes. Cette fois c'est faisable en terminale.
salut
c'est dommage ça commençait bien (ce qui est en gras) malheureusement ça se termine en queue de poisson en appliquant bêtement une formule sans réfléchir ....
d'autre part depuis le collège ::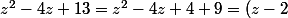^2 + 9)
et ensuite depuis la term ::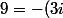^2)
....
Alors j'ai calculer Delta à la main puis vérifier à la calculette avec cette formule :
b² - 4.a.c J'optiens : (-4z)² - (4 * (z)² * 13) ce qui me donne delta = 36.
c'est dommage ça commençait bien (ce qui est en gras) malheureusement ça se termine en queue de poisson en appliquant bêtement une formule sans réfléchir ....
d'autre part depuis le collège ::
et ensuite depuis la term ::
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
L'énoncé, c'était : « Première question : Calculer son discriminant. Cette équation a-t-elle des solutions réelles ? » On ne demande pas de parler de solutions complexes conjuguées. Loustak a répondu en trouvant -36 : pas de solutions réelles.
Ensuite : « Vérifier pour tout nombre complexe z : z² - 4z + 13 = (z - 2 + 3i)(z - 2 - 3i) ». Pour ça il suffit de calculer le produit. Enfin : « En déduire que l'équation proposée a deux solutions complexes conjuguées que l'on déterminera. » Là il faut utiliser l'égalité pour exhiber les deux solutions conjuguées.
Ensuite : « Vérifier pour tout nombre complexe z : z² - 4z + 13 = (z - 2 + 3i)(z - 2 - 3i) ». Pour ça il suffit de calculer le produit. Enfin : « En déduire que l'équation proposée a deux solutions complexes conjuguées que l'on déterminera. » Là il faut utiliser l'égalité pour exhiber les deux solutions conjuguées.
(Hors-sujet)
Ah, ça oui !
Quand je résous une équation du 2nd degré sur les réels, j'aime bien écrire quelque chose comme :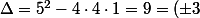^2) .
.
Et je trouve que ce serait utile de parler des racines carrées de Delta : Delta admet deux racines carrées, 3 et -3, donc il y a deux solutions, etc. Le cas général complexe serait alors similaire. (Bien sûr il faudrait bien distinguer « les » racines carrées de « la » racine carrée, laquelle ne serait alors plus très utile, ce qui ne me dérange pas.)
Ah, ça oui !
Quand je résous une équation du 2nd degré sur les réels, j'aime bien écrire quelque chose comme :
Et je trouve que ce serait utile de parler des racines carrées de Delta : Delta admet deux racines carrées, 3 et -3, donc il y a deux solutions, etc. Le cas général complexe serait alors similaire. (Bien sûr il faudrait bien distinguer « les » racines carrées de « la » racine carrée, laquelle ne serait alors plus très utile, ce qui ne me dérange pas.)
Robic a écrit:(Hors-sujet)
Ah, ça oui !
Quand je résous une équation du 2nd degré sur les réels, j'aime bien écrire quelque chose comme :.
Et je trouve que ce serait utile de parler des racines carrées de Delta : Delta admet deux racines carrées, 3 et -3, donc il y a deux solutions, etc. Le cas général complexe serait alors similaire. (Bien sûr il faudrait bien distinguer « les » racines carrées de « la » racine carrée, laquelle ne serait alors plus très utile, ce qui ne me dérange pas.)
insister sur le fait que pour tout nombre positif il existe deux nombres opposés dont le carré est ce nombre je suis bien d'accord .... mais/car malheureusement même en TS pour beaucoup
il est d'autre part évident qu'un travailleur manuel (comme moi) n'écrit jamais
mais pour faire prendre conscience à un automate que prendre 3 ou -3 lorsque d = 9 c'est la même chose .... bof vu (*)
l'homme possède tant de richesse ... et on le bride ... par des appendices qui lui font plus de tord qu'autre chose ... quelle tristesse ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
loustak a écrit:Bonjour,
Je suis en Terminal STI et on ma donner pour devoir un DM. Cependant je bloque à la première question :mur: .
Voici l'énoncé :
On considère l'équation z²-4z+13 = 0 ou z est un nombre complexe.
Première question : Calculer sont discriminent. Cette équation à t'elle des solutions réelles ?
Alors j'ai calculer Delta à la main puis vérifier à la calculette avec cette formule :
b² - 4.a.c J'optiens : (-4z)² - (4 * (z)² * 13) ce qui me donne delta = 36.
Vu que delta est positif l'équation à deux solutions réels et pas de solutions complexes, non ?
Seulement les questions suivantes sont :
Vérifier pour tout nombre complexe z : z² - 4z + 13 = (z - 2 + 3i)(z - 2 - 3i)
En déduire que l'équation proposée à deux solutions complexes conjuguées que l'on déterminera.
J'en déduit que à la première question j'aurais du trouvé un Delta négatif non ?
Merci de votre aide
Fais attention, un nombre z est dit complexe s'il s'écrit sous la forme z=a+ib avec a et b des réels.
Dans ton équation, tu confonds z et i. i est un nombre complexe particulier (a=0 et b=1) alors que l'énoncé te dit "z est un nombre complexe" donc quelconque (de la forme a+ib ou a et b peuvent valoir "n'importe quoi" tant qu'ils restent des réels.)
tabul a écrit:Fais attention, un nombre z est dit complexe s'il s'écrit sous la forme z=a+ib avec a et b des réels.
Dans ton équation, tu confonds z et i. i est un nombre complexe particulier (a=0 et b=1) alors que l'énoncé te dit "z est un nombre complexe" donc quelconque (de la forme a+ib ou a et b peuvent valoir "n'importe quoi" tant qu'ils restent des réels.)
l'énoncé est il mal conçu car il ne fait pas le lien explicite
entre
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
