► 1ere S : DM - Suites

par **Lauweep** » 12 Fév 2015, 17:25

Bonjour,

J'ai un DM sur les suites à faire pour la rentrée mais je bloque sur quelques questions... Voici l'énoncé :

Les services de la mairie d'une ville ont étudié l'évolution de la population de cette ville. Chaque année, 12,5 % de la population quitte la ville et 1 200 personnes s'y installent.
En 2012, la ville comptait 40 000 habitants.
On note Un le nombre d'habitants de la ville en l'année 2012 + n.

1) Déterminer u0, u1 et u2 :
J'ai trouvé :
u0 = 40 000
u1 = 36 200
u2 = 32875
Grâce à cette expression : [Un-(Un*12.5/100)]+1200

2) La suite (Un) est-elle géométrique ? Arithmétique ?
J'ai trouvé qu'elle n'était ni arithmétique ni géométrique, c'est normal ?

3) On admettra que la suite (Un) est définie par la relation de récurrence :
u0 = 40 000
Un-1 = 0,875*Un +1200 (Je crois qu'il y a une erreur et que c'est plutôt Un+1)

On considère alors l'algorithme suivant :

U prend la valeur 40 000
N prend la valeur 0
Tant que U > 10 000
N prend la valeur N +1
U prend la valeur 0.875*U+1200
Fin Tant que
Afficher N

a) Que représente la variable N affichée à la fin de l'algorithme ?
J'ai mis : N représente le plus petit rang de n pour lequel on a Un>10 000
(Je ne suis pas sûre que ce soit juste)

b) Que faudrait-il modifier dans l'algorithme si la population sortante n'était que de 10% (avec la même population rentrante) ?
Là je ne sais absolument pas... je me dis que ça a sûrement un lien avec 0,875 mais je ne vois pas comment faire :mur:

A partir de là je me suis arrêtée mais voici les questions suivantes :

4) On définit maintenant la suite (Vn) pour tout n appartenant à N par Vn=Un-9600
a) Démontrer que la suite est géométrique, préciser la raison et le premier terme.
b) En déduire une expression de Vn en fonction de n, puis une expression de Un en fonction de n.

5) En utilisant la méthode de votre choix, déterminer l'année au cours de laquelle la population de la ville sera pour la première fois inférieure à 10 000 habitants.
Là je pense simplement résoudre : Un<10 000 ou avec la calculatrice.

Merci d'avance pour votre aide !

par **annick** » 12 Fév 2015, 18:32

Bonjour,
pour un+1=0,875 un +1200, tu as raison.
Pour démontrer que Vn est géométrique, il faut que tu exprimes Vn+1 en fonction de Un+1, puis que tu fasses une mise en facteur pour essayer de retrouver Vn+1=qVn.

par **Lauweep** » 12 Fév 2015, 18:48

annick a écrit:Bonjour,
pour un+1=0,875 un +1200, tu as raison.
Pour démontrer que Vn est géométrique, il faut que tu exprimes Vn+1 en fonction de Un+1, puis que tu fasses une mise en facteur pour essayer de retrouver Vn+1=qVn.

En fait je dois faire : Vn+1= Un+1-9600 ?
Ce qui donne : 0.875*Un+1200-9600
= 0.875*Un-8400

Par contre à partir de là je ne sais pas trop quoi faire...
Je remarque qu'en faisant :
0.875*Un-8400=0
Un=9600

par **annick** » 12 Fév 2015, 19:15

On peut remarquer que :

Vn+1= 0.875*Un-8400 = 0,875 (Un-8400/0,875)

Vn+1=0,875(Un-9600)=0,875 Vn

D'où (Vn) est bien une suite géométrique.

par **Lauweep** » 12 Fév 2015, 19:29

Ah d'accord merci beaucoup !
Donc de raison q=0.875
et v0=40 000-9600= 30 400 ?

Pour ce qui est de la question 3)b) je viens de comprendre que 1-(12.5/100)=0.875
Donc pour 10% de personnes sortantes, ça devient 1-(10/100)=0.9
Donc on doit changer dans l'algorithme : 0.9*U+1200 ?

par **Lauweep** » 13 Fév 2015, 16:28

Quelqu'un pourrait m'éclairer s'il vous plait ? :)

par **mathelot** » 13 Fév 2015, 16:44

Lauweep a écrit:Donc on doit changer dans l'algorithme : 0.9*U+1200 ?

oui..................

par **Lauweep** » 13 Fév 2015, 16:49

Ok merci ! Est ce que tout ce que j'ai fait jusqu'à présent est bon ?
Par exemple, pour la 3)a) ?

par **Lauweep** » 13 Fév 2015, 16:53

Par contre autant la 5) je pense savoir quoi faire mais pour la 4)b) je ne sais vraiment pas...

par **mathelot** » 13 Fév 2015, 17:45

Lauweep a écrit:3) On admettra que la suite (Un) est définie par la relation de récurrence :
u0 = 40 000
Un+1 = 0,875*Un +1200 (1)

4) On définit maintenant la suite (Vn) pour tout n appartenant à N par Vn=Un-9600
a) Démontrer que la suite est géométrique, préciser la raison et le premier terme.

calcule le point fixe

tel que

(2)

tu dois trouver 9600.

en soustrayant (2) de l'égalité de récurrence, ça simplifie la constante 1200
et fait de

une suite géométrique

par **Lauweep** » 13 Fév 2015, 17:56

mathelot a écrit:calcule le point fixe tel que

(2)

tu dois trouver 9600.

en soustrayant (2) de l'égalité de récurrence, ça simplifie la constante 1200
et fait de une suite géométrique

Oula je n'ai jamais vu ni ce signe

ni ce qu'était un point fixe...
Ca reviendrait à faire ça ? :
0.875*Un-8400=0
Un=9600

Et à partir de là je fais 9600-1200 ? Désolée mais je n'ai pas bien compris votre explication :/

par **mathelot** » 13 Fév 2015, 18:17

l'équation est du 1er degré à une inconnue.

soustraie membre à membre les deux égalités de fonction affine.

Les constantes 1200 disparaissent.

par **Lauweep** » 13 Fév 2015, 18:41

mathelot a écrit: l'équation est du 1er degré à une inconnue.

soustraie membre à membre les deux égalités de fonction affine.

Les constantes 1200 disparaissent.

A ça y est j'ai compris ! Et effectivement je trouve bien que (Vn) est géométrique et de raison 0.875, merci !

Par contre Est-ce que cette réponse est juste :

Lauweep a écrit:a) Que représente la variable N affichée à la fin de l'algorithme ?
J'ai mis : N représente le plus petit rang de n pour lequel on a Un>10 000

Et pour la 4)b) je ne sais pas vraiment comment faire... Est ce que je dis simplement :
Un=0.875*n+1200
Or Vn=Un-9600
Donc Vn=(0.875*n+1200)-9600

Sauf que je crois que ce n'est absolument pas ça...

par **mathelot** » 13 Fév 2015, 19:07

soustraire a=c
de b=d

c'est écrire b-a=d-c

si on fait cette opération avec les deux égalités (1) et (2), on obtient
la formule de récurrence de (vn)

se rappeler le distingo entre fonction linéaire et fonction affine

par **mathelot** » 13 Fév 2015, 19:18

tu peux soustraire la 2ème égalité de la 1ère ? et réfléchir à ce que l'on obtient

par **Lauweep** » 13 Fév 2015, 19:21

Donc en gros il faut faire : (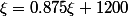

) - (Un+1 = 0,875*Un +1200) ?
Le truc c'est que je ne sais pas ce que représente \xi et pour moi c'est la même chose que Un+1... Pouvez vous m'expliquer davantage parce que je vois où vous voulez en venir mais ne sachant pas ce que représente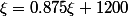

, je ne sais pas comment procéder :hum:

par **mathelot** » 13 Fév 2015, 22:03

Lauweep a écrit:mais ne sachant pas ce que représente , je ne sais pas comment procéder :hum:

c'est une inconnue d'une équation du 1er degré. la solution est 1600.

par **mathelot** » 13 Fév 2015, 22:09

erratum:

par **annick** » 13 Fév 2015, 23:32

Pour reprendre plus simplement :

(Vn) est une suite géométrique de raison q=0,875 et de premier terme V0=30400.

Or tu as du apprendre une formule qui te donne Vn en fonction de V0, de q et de n.

Ensuite, tu sais que Vn=Un-9600, donc tu peux exprimer Un en fonction de Vn (celui que tu viens de trouver en fonction de V0 et q).
Tu auras ainsi Un en fonction de n et cela te permettra de résoudre ton inéquation finale.

Il faudrait que tu arrives à bien comprendre ce genre de problème car il est très classique :
1) tu as une suite qui n'est rien de connu
2) tu as une suite qui dépend de la première et que l'on trouve géométrique par exemple.
3) on exprime alors cette suite en fonction de n.
4) on revient alors à la première suite et on peut alors l'exprimer en fonction de n, ce qui n'était pas le cas au début.

par **mathelot** » 14 Fév 2015, 08:59

Lauweep[B a écrit:3) On admettra que la suite (Un) est définie par la relation de récurrence :
u0 = 40 000
Un-1 = 0,875*Un +1200[/B]4) On définit maintenant la suite (Vn) pour tout n appartenant à N par Vn=Un-9600

si soustraire les égalités t'est trop compliqué , on peut également écrire

► 1ere S : DM - Suites

► 1ere S : DM - Suites

Qui est en ligne