Cette question était importante, mais la réponse que j'attendais était
oui ou
non. Est-ce que tu sais faire le calcul, oui ou non ? C'était pour savoir si tu avais déjà vu le calcul de ce genre de somme, ou en tout cas si tu étais capable de faire le lien avec un cours que tu aurais déjà vu.
Si tu réponds oui, dans ce cas je suis rassuré, c'est que tu as compris le truc.
Si tu réponds non, j'en déduis qu'il faut t'aider à calculer ce genre de chose. Mais je ne vais pas t'aider si c'est inutile.
D'après ta réponse ci-dessous : non. OK. Dans ce cas voici quelques « rappels » :
1) Somme des termes d'une suite géométrique :
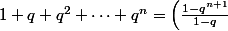)
2) Série géométrique (si |q| < 1) :
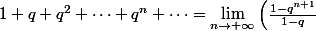 = \frac{1}{1-q})
En multipliant à gauche et à droite par q :

C'est ce genre de résultat qui sert dans cet exercice. Est-ce que tu as déjà vu ce genre de chose ? (Pour faire cet exercice, il faudrait.)
