Exercies: équations, probabilités, fonctions

[Yocz]

Bonjour, voici les exercices que j'ai a réalisé dans le cadre d'un dm:

I. Equations diverses

a) (j'ai trouvé: )

b) (j'ai trouvé )

c)

d) avec deux méthodes:
•En utilisant la factorisation
•En commençant par résoudre


II. Reprendre le TP 1 p 201 commencé en classe

Répondre par écrit aux questions du B
Répondre aux questions 2) et 3) du C) (justifier pour le 3)


On donne une copie d'écran d'un affichage possible:



III.

Merci pour vos réponses!

[Rizmoth]

Bonjour,

Commençons par le début : I

a) Je vois que tu as développé la forme factorisée qui t'était donnée dans l'équation. Ici, ce n'est pas ce qu'on te demande. Dans une équation, il y a une inconnue, (x en l'occurence), et ton but, c'est trouver sa (ou ses) valeurs possibles. Ici, la forme que tu donnes n'est qu'une autre forme de la même équation, mais en soi, tu n'as pas terminé le travail. A ce stade, il y a deux possibilités :

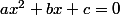
1/ Soit tu utilises ta forme développée. Tu commences par réunir les termes en , les termes en et les termes constants. L'équation prend la forme : et tu te retrouves dans le cas d'un trinôme du second degré. Soit, c'est solvable.

2/ Soit tu utilises la forme factorisée initiale. Je remarque souvent auprès des élèves de lycée que le traitement du produit nul n'est pas forcément automatique. Es-tu familiarisé avec ça ? Voilà ce qu'il faut retenir :
Un produit A x B est nul si et seulement A = 0 ou B = 0 (ou éventuellement les deux).

Ta première équation est exactement un cas de produit nul. Et dans ce cas, c'est la méthode 2 qui est la plus simple.


Déjà, on peut diviser par 3 des 2 côtés. 0/3, ça fait toujours zéro...

Voilà le produit nul. On a une équation de la forme A x B = 0 avec :
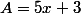
et
Pour trouver les solutions d'une telle équation, en vertu du théorème, cela revient à résoudre ces deux "sous-équations" :


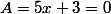
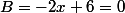
Chacune admet une solution. Et l'équation de départ en admet du coup...2 !

Jusque là, on est d'accord ?

[tototo]

Bonjour, voici les exercices que j'ai a réalisé dans le cadre d'un dm:



Merci pour vos réponses!

1a) x=-3/5 ou x=3
b) ((x-4)(x+4)/-(x-4))=0 x=-4

[Rizmoth]

Ouais effectivement, au terme de ma longue litanie, on tombe sur le résultat avancé par tototo...

A voir si l'explication intéresse plus l'auteur que l'éjection de réponses. :)

[Yocz]

OK pour le a)

En revanche je n'ai pas trop compris pour le b)

[tototo]

Bonjour, voici les exercices que j'ai a réalisé dans le cadre d'un dm:



Merci pour vos réponses!

d)
en utilisant la factorisation:
(2x-5-racine(5))(2x-5+racine(5))=0
x=(5+)/2 ou x=(5-)/2

[tototo]

Bonjour, voici les exercices que j'ai a réalisé dans le cadre d'un dm:



Merci pour vos réponses!

d) en commencant par résoudre X^2=5 x=-racine(5) ou x=+racine(5)
en remplacant X par 2x-5 on obtient:
2x-5=-racine(5) ou 2x-5=+racine(5)
x=(-racine(5)+5)/2 ou x=(+racine(5)+5)/2

[tototo]

OK pour le a)

En revanche je n'ai pas trop compris pour le b)

Bonjour Yocz,

Pour la b) on factorise le numérateur afin d’énlever le dénominateur(il ne reste que -1) et ainsi de résoudre l'équation.

[tototo]

Bonjour, voici les exercices que j'ai a réalisé dans le cadre d'un dm:



Merci pour vos réponses!

1. a0 donc b>0 car ax=0 pour x=0.
3.On obtient le systeme :
b=a^2
2a+b=0

2a+a^2=0 a(2+a)=0 a=0 ou a=-2

S={(0;0);(-2;4)}

[Yocz]

Ok pour le III.

Mais pour le d) que signifie racine(5), je n'arrive pas trop à déchiffrer :/

[tototo]

Bonjour, voici les exercices que j'ai a réalisé dans le cadre d'un dm:



Merci pour vos réponses!

ENT(6*ALEA()+1) qui représente un entier naturel entre 1 et 6
donc ENT(ALEA()+0,1) représente un nombre soit 0 soit 1 avec la même probabilité.
SOMME(A1;A22) représente la somme des résultats des 22 premiers jour.
on compte les resultat sur des périodes de 22 jours.
MAX(B22;B365) affiche le maximum de fois ou sur une période de 22 jours on est tombe sur le 1 (=rouge).
On calcule la fréquence pour laquelle le max sur 22 jours par ans est supérieur à 5 sur 50 tirages.

[tototo]

Ok pour le III.

Mais pour le d) que signifie racine(5), je n'arrive pas trop à déchiffrer :/

racine(5)= sans Latex.
Dsl je n'ai pas écrit en Latex en espérant que ça soit plus claire.

[tototo]

Bonjour, voici les exercices que j'ai a réalisé dans le cadre d'un dm:



Merci pour vos réponses!

La propabilité se stabilise vers l'asymptote horizontale.

[Yocz]

Bonsoir, quelqu'un pourrait-il m'éclairer sur le II ? svp Merci