Bonjour.
D'après la Relativité Générale, si on pose des masses pondérables

au voisinage d'un corps d'épreuve ayant la masse inertielle

, cette dernière augmente suivant la loi
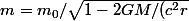})
, ...(1)
où

et

sont la constante de Newton et la célérité de lumière .
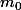
étant la valeur de

en l'absence de toute masse pondérable (
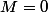
ou
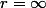
).
Afin de réconcilier la Relativité Générale avec le principe de Mach, Telkamp [arXiv1207.4717;1404.4046] fit la suggestion de substituer la relation (1) par
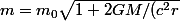})
. ...(2)
Puisque l'éq.(2) possède la même approximation de l'éq.(1):
))
elles conduisent aux mêmes résultats.
Maintenant, on se propose de comparer les densités effectives
)
obtenues des résultats ``exacts'' des deux relations quand la masses pondérable est un disque plat de rayon

avec une densité ``apparemment constante''
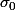
tandis que la particule d'épreuve
p est un point du disque à la distance

du center O.
Suivant l'éq. (1) pour tout élément de masse
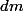
à la distance

du centre
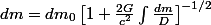
, ...(3)
où
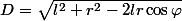
.
Puisque l'élément de surface vérifie
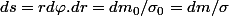
,
on peut réecrire l'éq.(3) sous
=\sigma_{0}\left[ 1-\frac{2G}{c^{2}}\int^{2\pi}_{0}\int^{R}_{0}\frac{\sigma(r)r.dr.d\varphi}{\sqrt{l^{2}+r^{2}-2lr\cos \varphi}} \right]^{-1/2})
. ...(4)
Par la meme voie, l'éq.(2) conduit à
=\sigma_{0}\left[ 1+\frac{2G}{c^{2}}\int^{2\pi}_{0}\int^{R}_{0}\frac{\sigma(r)r.dr.d\varphi}{\sqrt{l^{2}+r^{2}-2lr\cos \varphi}} \right]^{1/2})
. ...(5)
Finalement, l'extraction de
)
des relations (4) et (5) permet
de calculer la masse
)
à l'intérieur du rayon

:
=2\pi\int^{r}_{0}\sigma(l)ldl)
.
Il est possible que cette
)
vérifie la courbe des vitesses de rotation galactiques sans avoir recours à une masse cachée, c-a-d:
^{2}=\frac{Gm(r)}{r})
.
Le problème majeur qui persiste c'est comment extraire

des éqs. (4) et (5)?
Merci de votre aide. Cordialement.
