Bonjour, j'aurais besoin d'un coup de main pour faire l'exercice suivant :
Soit

la fonction sur

définie par :
[CENTER]
=\frac{1}{(1-z^2)(1-z^3)})
[/CENTER]
1°) On me demande de montrer que

admet un développement en série entière au voisinage de

.
2°)a) Calculer de deux manière différentes ce développement en série entière.
b) Calculer alors le cardinal de
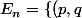\in \mathbb{N}^2 \mid 2p+3q=n \},n\in \mathbb{N})
.
1°) Avant tout, j'ai commencé par dire que

est définie sur

. Je sais que les fonctions

et

sont développable en série entière sur le disque ouvert
)
. Donc le produit

de ses deux fonctions admet un développement en série entière sur
)
et ainsi, il existe un voisinage

de

dans lequel

est développable en série entière.
(Ai-je bon ?)
2°)a) Je bloque à partir de là...
Merci d'avance pour votre aide :+++:
