Mathématiques TS les nombre complexes

[sarah59495]

Bonjour à tous et à toutes,
mon prof de maths, nous a donné un DM que je ne comprends pas et que je n'arrive pas à faire. Sachant que je n'ai aucune cours. Je suis dans une véritable impasse. Est-il possible d'obtenir votre aide?
Pour ceux qui sont intéressés, voici le sujet:

On dit que P est un polynôme a coefficient réel, si pour tout nombre complexe z, on a:
P(z)=a0+a1z+a2z²+ ... + anz^n (le 1er nombre est en indice) avec a(indice)i appartient IR pour tout entier i<(ou égale)n et a(indice)n différent de 0. On appelle n le degré du polynôme.

1) On considère un polynôme a coefficient réel, de degré impair
a)Etudier les limites de P(x) en plus ou moins infini en fonction du signe de a(indice)n
b)En déduire, en justifiant soigneusement, que tout polynôme de degré impair possède au moins une racine réelle

2) D'après le cours, (que je n'ai pas) expliquer pourquoi on peut affirmer, que si z est une racine d'un polynôme de 2nd degré a coefficients réels, alors son conjugué z(barre) est aussi une racine du polynôme.

3)Généralisons: Soit P, défini par P(z)=a0+a1z+a2z²+ ... + anz^n (le 1er nombre est en indice), un polynôme a coefficient réel
a)Si z est un nombre complexe, exprimer P(z)(tout est sous la barre), en fonction des a(indice)i et de z(barre)
b)Si z est un nombre complexe, exprimer P(z)(là il n'y a que z sous la barre), en fonction des a(indice)i et de z(barre)
c)Montrer alors que si P admet le nombre z, comme racine, alors z(barre) est aussi une racine de P

4)On sait qu'un polynôme P de degré 5, possède les 2 racines suivantes: (1/2)+i(racine3/2) et i
On sait également que P(0)=6 et que a(indice)5=2
Trouver toutes les racines de P, ainsi que la forme développée de P
Il faudra rédiger, afin de montrer l'enchaînement de la réflexion



Voici mon sujet, j'espère que vous pourriez m'aider, m'orienter, m'expliquer
Merci d'avance

[Carpate]

Bonjour à tous et à toutes,
mon prof de maths, nous a donné un DM que je ne comprends pas et que je n'arrive pas à faire. Sachant que je n'ai aucune cours. Je suis dans une véritable impasse. Est-il possible d'obtenir votre aide?
Pour ceux qui sont intéressés, voici le sujet:

On dit que P est un polynôme a coefficient réel, si pour tout nombre complexe z, on a:
P(z)=a0+a1z+a2z²+ ... + anz^n (le 1er nombre est en indice) avec a(indice)i appartient IR pour tout entier i<(ou égale)n et a(indice)n différent de 0. On appelle n le degré du polynôme.

1) On considère un polynôme a coefficient réel, de degré impair
a)Etudier les limites de P(x) en plus ou moins infini en fonction du signe de a(indice)n
b)En déduire, en justifiant soigneusement, que tout polynôme de degré impair possède au moins une racine réelle

2) D'après le cours, (que je n'ai pas) expliquer pourquoi on peut affirmer, que si z est une racine d'un polynôme de 2nd degré a coefficients réels, alors son conjugué z(barre) est aussi une racine du polynôme.

3)Généralisons: Soit P, défini par P(z)=a0+a1z+a2z²+ ... + anz^n (le 1er nombre est en indice), un polynôme a coefficient réel
a)Si z est un nombre complexe, exprimer P(z)(tout est sous la barre), en fonction des a(indice)i et de z(barre)
b)Si z est un nombre complexe, exprimer P(z)(là il n'y a que z sous la barre), en fonction des a(indice)i et de z(barre)
c)Montrer alors que si P admet le nombre z, comme racine, alors z(barre) est aussi une racine de P

4)On sait qu'un polynôme P de degré 5, possède les 2 racines suivantes: (1/2)+i(racine3/2) et i
On sait également que P(0)=6 et que a(indice)5=2
Trouver toutes les racines de P, ainsi que la forme développée de P
Il faudra rédiger, afin de montrer l'enchaînement de la réflexion



Voici mon sujet, j'espère que vous pourriez m'aider, m'orienter, m'expliquer
Merci d'avance

1) Indice :
P(x) est continue sur R
Pour n pair, (et donc ) quand
Mais pour n impair quand et quand

[mathelot]

sans cours, ça relève de l'exploit.


i)

On applique une généralisation du TVI pour obtenir que P s'annule.


ii) soit z une solution, qui annule P



on conjugue





donc les racines vont par paires de conjugués.


exemple

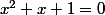à coefficients réels:

j et sont racines.

lien