bonjour,
Je voudrais savoir à quoi correspond intuitivement la différentielle d'une fonction notée df, physiquement et mathématiquement .. :cry:
Differentielle
4 messages
- Page 1 sur 1
bonjour,
mathématiquement et physiquement, une différentiellle est pareillle qu'une dérivée.
C'est une apppplication linéaire , à laquelle si on rajoute le point de contact avec la surface,
fera un espace tangent.,
exemple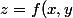=x^3y^4)
en x0,y0 on donne un petit accroisssement à la variable
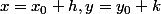
on remplace dans f, on développpe, on examine la partie linéaire
en (h,k)
=(x_0^3+3x_0^2h+3x_0h^2+h^3)(y_0^4+4y_0^3k+6y_0^2k^2+4y_0k^3+k^4))
=f(x_0,y_0)+h( 3x_0^2y_0^4)+k(4y_0^3x0^3)+o(h,k))
de même queh) est linéaire en h mais sa coordonnée
est linéaire en h mais sa coordonnée
dans l'espace tangent depend de x, pareil pour les différentiellles
df(h,k)=h( 3x0^2y0^4)+k(4x0^3y0^3) est la partie linéaire en (h,k).
commme on approche la fonction au voisinage de x0,y0,
on note
df(x0,y0)(h,k)=h( 3x0^2y0^4)+k(4y_0^3x_0^3) est la partie linéaire en (h,k).
Z=f(x0,y0)+df(x0,y0)(X,Y)
est l'équation du plan tangent
de la surface d'équation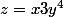 , le point de tangence est (x_0,y_0)
, le point de tangence est (x_0,y_0)
En phys, c'est pareil mais h=dx(h) est noté plutôt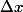 ,
,
c'est l'accroissement "brut de fonderie", par exemple
on n'écrit pas) pour les accroissements physiques.
pour les accroissements physiques.
remarque: historiquement, on ne savait pas si
 est une bonne notation ou non.
est une bonne notation ou non.
mathématiquement et physiquement, une différentiellle est pareillle qu'une dérivée.
C'est une apppplication linéaire , à laquelle si on rajoute le point de contact avec la surface,
fera un espace tangent.,
exemple
en x0,y0 on donne un petit accroisssement à la variable
on remplace dans f, on développpe, on examine la partie linéaire
en (h,k)
de même que
dans l'espace tangent depend de x, pareil pour les différentiellles
df(h,k)=h( 3x0^2y0^4)+k(4x0^3y0^3) est la partie linéaire en (h,k).
commme on approche la fonction au voisinage de x0,y0,
on note
df(x0,y0)(h,k)=h( 3x0^2y0^4)+k(4y_0^3x_0^3) est la partie linéaire en (h,k).
Z=f(x0,y0)+df(x0,y0)(X,Y)
est l'équation du plan tangent
de la surface d'équation
En phys, c'est pareil mais h=dx(h) est noté plutôt
c'est l'accroissement "brut de fonderie", par exemple
on n'écrit pas
remarque: historiquement, on ne savait pas si
mathelot a écrit: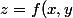=f(x_0,y_0)+h( 3x_0^2y_0^4)+k(4y_0^3x0^3)+o(x,y))
Salut !
J'aime bien l'explication, elle donne un bon sens aux différentielles qui ne sont pas toujours évidentes à cerner...
Par contre, ce n'est pas
Sinon, pour dire les choses au "premier niveau", une différentielle, c'est regarder comment agit une fonction (en maths), une trajectoire par exemple (en physique) dans un laps (de temps par exemple) très court..., notamment de savoir le rapport entre ce laps et l'évolution de la fonction.
Si je prends le cas très simple de la parabole, avec f(x) = x² et f'(x)= 2x.
En 1 par exemple, on a f(1) = 1 et f'(1) = 2.
Ce qui veut dire que pour x proche de 1, donc pour 1 + h avec h proche de 0, on a f(1+h) qui vaut environ f(1) + f'(1)h c'est à dire ici 1 + 2h...
Voilà, je te donne la version de base, celle dont on nous parle, un peu, au lycée :ptdr:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
