Je suis en détresse profonde. (Seconde)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 20:14
par PandoraL » 11 Jan 2015, 20:14
Bonjour et bonne année!
Cela fait plus de quatre semaines que je bloque sur mon devoir maison. Je repousse toujours l'échéance pour le rendre mais, malgré ma persévérance je ne comprends absolument rien. Etant une élève vraiment très médiocre en mathématique, je me tourne vers vous.
http://www.hostingpics.net/viewer.php?id=531809109131431529749740644450275065961n.jpg(L'image de mon devoir est hébergé ici.)
J'ai réellement du mal avec le petit 2 de l'exercice 1 et également les deux dernières inéquations de l'exercice 2. J'ai vraiment besoin de vous, s'il-vous-plaît.


Merci infiniment!
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
 par maxnihilist » 11 Jan 2015, 20:25
par maxnihilist » 11 Jan 2015, 20:25
Bonjour,
Pour la question 2a) du premier exercice, tu vois que le point B se situe sur AE et que la distance de AE est de 4. Que peux-tu déduire de la distance AB ? Elle est inférieure ou égale à .. ? Tu viens de déduire la borne supérieure de la distance AB.
Ensuite, nous parlons de distance, c'est donc forcément positif ? Tu viens de déduire la borne inférieure de AB.
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 20:31
par PandoraL » 11 Jan 2015, 20:31
maxnihilist a écrit:Bonjour,
Pour la question 2a) du premier exercice, tu vois que le point B se situe sur AE et que la distance de AE est de 4. Que peux-tu déduire de la distance AB ? Elle est inférieure ou égale à .. ? Tu viens de déduire la borne supérieure de la distance AB.
Ensuite, nous parlons de distance, c'est donc forcément positif ? Tu viens de déduire la borne inférieure de AB.
C'est vraiment très gentil de m'avoir répondu!
Même si je ne comprends pas vraiment.. Pour moi la distance de AB est inférieure à AE?
Je suis désolée, je suis vraiment nulle et pas douée >.<
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
 par maxnihilist » 11 Jan 2015, 20:32
par maxnihilist » 11 Jan 2015, 20:32
La distance AB est inférieure ou égale à AE oui et forcément positive ou nulle (on imagine difficilement une distance négative).
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
 par maxnihilist » 11 Jan 2015, 20:35
par maxnihilist » 11 Jan 2015, 20:35
Pour la 2b)
Air d'un carré = (côté)²
Du coup la somme des deux aires donne : x² + (4 - x)²
x étant la distance AB et 4 - x la distance BE.
Tu as ensuite une inéquation à résoudre
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 20:43
par PandoraL » 11 Jan 2015, 20:43
maxnihilist a écrit:La distance AB est inférieure ou égale à AE oui et forcément positive ou nulle (on imagine difficilement une distance négative).
D'accord.
Mais, je ne comprends pas ce qu'elle a voulu nous par "A quel intervalle appartient x". Qu'est-ce que ça veut dire concrètement.
Je veux dire, je comprends ce que vous voulez dire par la distance AB est inférieure ou égale à AE mais, comment on peut réellement le représenter?
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
 par maxnihilist » 11 Jan 2015, 20:45
par maxnihilist » 11 Jan 2015, 20:45
x représente la distance AB et doit donc être compris entre 0 et 4.
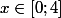
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
Dude5219
- Membre Naturel
- Messages: 24
- Enregistré le: 28 Déc 2014, 15:51
-
 par Dude5219 » 11 Jan 2015, 20:54
par Dude5219 » 11 Jan 2015, 20:54
PandoraL a écrit:Bonjour et bonne année!
Cela fait plus de quatre semaines que je bloque sur mon devoir maison. Je repousse toujours l'échéance pour le rendre mais, malgré ma persévérance je ne comprends absolument rien. Etant une élève vraiment très médiocre en mathématique, je me tourne vers vous.
http://www.hostingpics.net/viewer.php?id=531809109131431529749740644450275065961n.jpg(L'image de mon devoir est hébergé ici.)
J'ai réellement du mal avec le petit 2 de l'exercice 1 et également les deux dernières inéquations de l'exercice 2. J'ai vraiment besoin de vous, s'il-vous-plaît.


Merci infiniment!
Bonjour,
2.a) Si on instaure un ordre sur [AE] ; on peut dire que


2.b) Si A représente l'aire, la question peut être formulée comme : Déterminer x pour que
+A(BEFG)>10)
^2>10)
En espérant t'avoir aidé. :++:
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 20:54
par PandoraL » 11 Jan 2015, 20:54
maxnihilist a écrit:x représente la distance AB et doit donc être compris entre 0 et 4.
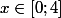
Alors si j'ai bien compris, c'est parce que AE = 4? Mais, pourquoi 0?
Je m'excuse de vous embêter mais, c'est pas le tout d'avoir des réponses toutes prêtes, j'aimerai comprendre..
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
 par maxnihilist » 11 Jan 2015, 20:59
par maxnihilist » 11 Jan 2015, 20:59
Il s'agit d'une distance.
Il serait difficile de dire que la distance séparant ton lycée à chez toi est de - 2km. C'est forcément positif.
Et comme "Dude5219" a dit, c'est compris entre [AA ; AE]
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 21:03
par PandoraL » 11 Jan 2015, 21:03
Donc, je note dans ma tête qu'une distance est forcément positive.
Mais, je me demandais si par exemple, au hasard, une intervalle pouvait contenir quelque du genre ->[-3;5] ou même deux négatifs?
Pour l'exercice 2, les inéquations, j'ai aussi vraiment du mal.
On doit bien faire basculer les nombres de l'autre côté?
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 21:03
par PandoraL » 11 Jan 2015, 21:03
En tout cas, merci beaucoup pour votre aide! Vraiment, vraiment!
-
maxnihilist
- Membre Relatif
- Messages: 166
- Enregistré le: 17 Fév 2013, 16:24
-
 par maxnihilist » 11 Jan 2015, 21:06
par maxnihilist » 11 Jan 2015, 21:06
Un intervalle peut effectivement être borné par deux nombres négatifs.
Il y a trois sortes de mensonges: les mensonges, les sacrés mensonges et les statistiques.
M. Twain
-
Vestiaz
- Messages: 6
- Enregistré le: 11 Jan 2015, 20:59
-
 par Vestiaz » 11 Jan 2015, 21:09
par Vestiaz » 11 Jan 2015, 21:09
Alors Oui, un intervalle peut avoir comme bornes deux nombres négatifs. [-2;-1].
Mais comme dit précédemment, dans ton cas ce n'est pas possible.
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 21:12
par PandoraL » 11 Jan 2015, 21:12
D'accord mais, admettons que plus tard, je rencontre un intervalle avec des négatifs, ça influera sur mon résultat final? Parce que ma prof, (ou du moins, je le comprends comme ça >.<) de mettre un signe infini après chaque intervalle a deux nombres négatifs.
-
Dude5219
- Membre Naturel
- Messages: 24
- Enregistré le: 28 Déc 2014, 15:51
-
 par Dude5219 » 11 Jan 2015, 21:12
par Dude5219 » 11 Jan 2015, 21:12
PandoraL a écrit:Donc, je note dans ma tête qu'une distance est forcément positive.
Mais, je me demandais si par exemple, au hasard, une intervalle pouvait contenir quelque du genre ->[-3;5] ou même deux négatifs?
Pour l'exercice 2, les inéquations, j'ai aussi vraiment du mal.
On doit bien faire basculer les nombres de l'autre côté?
Un intervalle peut contenir des valeurs négatives, mais dans le cadre de ton exercice non. Par convention, une distance est au moins supérieur ou égale à 0 c-à-d qu'elle n'est pas négative.
2. Oui, il faut faire basculer les nombres du même côté que les inconnus, ensuite réduire au même dénominateur. Mais avant ça, commence par déterminer l'ensemble de définition.
:++:
-
Vestiaz
- Messages: 6
- Enregistré le: 11 Jan 2015, 20:59
-
 par Vestiaz » 11 Jan 2015, 21:17
par Vestiaz » 11 Jan 2015, 21:17
Pour ce qui est de tes inéquations, pour la 2.3) il faut que tu fasses ce qu'on appelle une disjonction des cas.
Tu veux faire passer le x-2 de l'autre coté, le seul problème c'est que multiplier par un nombre négatif change le signe de l'inéquation ( > devient < et inversement).
Du coup il faut que tu regardes dans quel cas x-2 est négatif, et dans quel cas il est positif.
Et pour la seconde, il suffit de faire un tableau de signe, je ne sais pas si vous en faites encore.
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 21:38
par PandoraL » 11 Jan 2015, 21:38
Je suis désolée mais, disjonction? Je n'ai jamais entendu ce terme là..
Si, j'ai bien compris je dois faire passer tout les nombres de l'autre côté, ça veut dire que le +1 bascule avec le 4 ce qui fait 4-1 et je fais passer le -2 avec le 3 ce qui fait 3+2?
-
Vestiaz
- Messages: 6
- Enregistré le: 11 Jan 2015, 20:59
-
 par Vestiaz » 11 Jan 2015, 21:54
par Vestiaz » 11 Jan 2015, 21:54
Disjonction ça veut dire que tu dois traiter plusieurs cas, ici x-2 > 0 et x-2 < 0.
Je te donnais juste le nom "scientifique" pour ça.
Et pour répondre a ta question non. Tu n'as pas le droit de faire sortir le +1 et le -2 de cette façon. Ce que tu peux faire, c'est multiplier les deux membres (celui à gauche et celui à droite de l'inégalité) par le même nombre. Mais il faut faire attention au signe du nombre par lequel tu multiplies. Si jamais il est négatif il change le signe de l'inégalité.
Dans ton cas, il faut que tu commences par multiplier x+1 / x-2 et 4 / 3 par à la fois 3 et x-2. Comme ça tu retombes sur une inéquation plus simple (c'est à dire, sans fraction). Donc apres cette étape ça se résout comme les deux premières. Mais encore une fois, multiplier par 3, qui est positif ne change pas le signe car 3 est positif, mais tu ne connais pas le signe de x-2. Il peut etre positif ou négatif suivant les x. Donc tu traites le cas ou x-2 est positif, ce qui te donnera une inéquation, et un autre cas ou x-2 est négatif qui te donnera une toute autre équation.
Compris ?
-
PandoraL
- Messages: 9
- Enregistré le: 11 Jan 2015, 19:49
-
 par PandoraL » 11 Jan 2015, 21:59
par PandoraL » 11 Jan 2015, 21:59
Si j'ai bien compris = x+1 / x-2 = -2
4/3 = 12
et 4 / x- 2 = -2?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
