Otimisation Contrainte

[hari05]

Excusez moi aidez moi, je voudrais toutes les détail possible car sa m'aidera pour réviser pour le partiel.


Optimum contraint d'une fonction de plusieurs variables

Exercice 1

Trouvez le minimum contraint de la fonction f(x.y)=2x²+y² sous la contrainte g(x.y)=x+y-1=0, par la méthode de substitution de y de la contrainte g dans la fonction objectif f.

Exercice 2

En utilisant la méthode des multiplicateurs de Lagrange, trouvez l'extremum contraint de la fonction
f(x.y)=2x²+y² sous la contrainte g(x.y)=x+y=1. Les conditions du deuxième ordre sont requises.

Exercice 3

En utilisant la méthode des multiplicateurs de Lagrange, trouvez le minimum contraint de la fonction
f(x.y.z)=2xy+6yz+8xz sous la contrainte g(x.y.z)=xyz= 12.000.
Les conditions du deuxième ordre ne sont pas requises.

Exerice 4

Soit la fonction f(x.y)=x²+y²+xy
a) Déterminez les extrema de f
b)Même question en considérant que x et y sont désormais liées par la contrainte x+y=1. Examinez les conditions du deuxième ordre et concluez
c)Si f était une fonction d'utilité, que signifierait alors la recherche de ces deux extrema ?

Execice 5

Déterminez et précisez la nature des extrema des deux fonctions suivantes :
a) f1(x.y)=ln(x-y) sous contrainte que x²+y²=2
b)f2(x.y)=xy sous contrainte que x²+y²=2

[capitaine nuggets]

Salut !

Exercice 1

Si on a la contrainte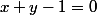 alors 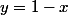donc trouver le minimum de revient à trouver le minimum de la fonction :+++: