paquito a écrit:Considérons l'inégalité

donc g est décroissante pour
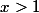
; or
1)
; il n'y a pas donc de suite croissante et dans tout les cas

converge vers

.
Il y a un petit truc que je ne saisis pas. Le raisonnement du début OK, mais pourquoi commencer par :

? (c'est fondamentalement pareil pour la recherche, je sais). Car après, quand tu enchaînes dans le raisonnement, tu dis :
Il en résulte que si

,

; par conséquent une éventuelle suite croissante serait majorée par

donc serait convergente
Moi je ne vois qu'une suite décroissante et minorée par 3 ici... Tu peux m'éclairer ? Ou alors c'est moi qui suis réveillé depuis trop peu de temps, et le raisonnement est de prendre du coup la contraposée, et alors annoncer ce que tu viens de dire. A la première lecture, je n'avais pas tilté. C'est bien ça ?
Remarques: il y a un corrigé sur le net, mais il est délicat;je me suis inspiré d'une solution plus claire trouvée par ben qui, je ne sais pas comment il fait, trouve toujours une solution géniale.
Normalement, cet exercice est destiné à des élèves de T°S, mais évidemment, ce sont essentiellement des élèves de grands lycées parisiens où on fait la moitié du programme de sup en terminale qui ont une petite chance. A côté d'un exo du concours général, un exo des olympiades, c'est pour les enfants.
Il y a quelques années, j'ai rencontré une de nos médailles Fields, Jean Christophe Yoccoz;cursus: 1° du concours général, 1° du concours d'entrée à l'E.N.S., 1° de l'agrégation suivi d'une thèse très brillante faite dans la foulée!!!
Il est clair que ces élèves très privilégiés constituent une minorité sans cesse plus restreinte.
C'est presque décourageant, mais non, je continue à chercher sur tout problème qui me semble abordable, et je m'améliore... tout doucement

Rien que log, il va doucement, mais il va en l'infini. Mon seul problème restera donc de trouver comment vivre éternellement... :ptdr:
