Pour prove le statement suivante , ce qu'on appelle P(n), demeurre vrai pour tout entier natruel n:
^{n}\le \dfrac{1}{1-\alpha})
mon preuve que P($n$) est vrai pour chaque entier naturel $n$ procedont comme suit :
**Basis:**
Montrons que notre statement est valable pour

.
P($1$) revient à la statement:
^{1}\le \dfrac{1}{1-\alpha})
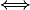
\le 1)
comme
 \longrightarrow 0\le \alpha < 1 \longrightarrow 0\le \alpha^2 < 1 \longrightarrow -1 \le -\alpha^2 < 0 \longrightarrow 0 \le 1-\alpha^2 < 1)
donc le statement est vrai pour $n=1$. donc P($1$) est bien vrai
**Inductive step:**
Montrons que P($n$) valable ,donc P($n+1$) l'est aussi . Cela peut être fait comme suit.
supposons que P($n$) vrai . il faut donc de montrer que P($n+1$) est vrai , c'est a dire :
je bloque ici
^{n+1}\le \dfrac{1}{1-\alpha})