Interpolation linéaire et tableau de valeurs

[Cynthia37200]

[img][IMG]http://img15.hostingpics.net/pics/22177410881413385309911638895566754345n.jpg[/img][/IMG]


Alors tout d'abord je vous souhaite une bonne année 2015 ainsi qu'un bon réveillon

Deuxièmement j'aimerai beaucoup que quelqu'un m'explique la notion d'interpolation linéaire que je ne comprends absolument pas. Par ailleurs j'ai un exercice à faire sur ça avec les questions suivantes où je bloque depuis lundi :mur: . J'espère que vous allez pouvoir m'aider à comprendre:

-Par interpolation linéaire estimez estimez f(3/2) puisque l'on ne connaît pas cette valeur (c=3/2)
-Par interpolation linéaire estimez estimez f(3) puisque l'on ne connaît pas cette valeur (c=3)
--Par interpolation linéaire estimez la solution f(x)=0 qui est supérieure à 4.

[laetidom]

Salut Cynthia,

Je te fais le 1) (si je me souviens bien) : (déjà trace un graphe avec les données du tableau et regarde l'allure de la courbe obtenue pour voir si les résultats que tu va calculer sont sur la courbe ou en dehors...cohérence oblige !)

f(3/2)=?

pour passer en x de 1 à 2 on a une longueur de 1

donc à 1 (en x) on fait correspondre quoi en y ?

calcul : on fait correspondre la longueur en valeur absolue de Y1-Y2=(1/12)+(4/3)=17/12

donc à 1 correspond 17/12

et à 0.5 correspond x = ? (0.5 est à la moitié entre 1 et 2, donc correspond à 3/2)

REGLE DE TROIS : x=0.5.(17/12)=17/24


17/24 est une valeur de y depuis l'ordonnée de 1

donc ce qu'on cherche c'est donc (1/12) - (17/24) = -15/24

et -15/24=-0.625, d'après moi c'est bien sur ma courbe tracée à main levée, donc ça devrait correspondre....sauf distraction vu le contexte de réveillon de la st sylvestre ! ! ! ...........

donc f(3/2)=-15/24 par interpolation linéaire entre les points d'abscisses 1 et 2
---------------------------

Bonne fête à tous ! ! !.......................

[Cynthia37200]

Salut Cynthia,

Je te fais le 1) (si je me souviens bien) : (déjà trace un graphe avec les données du tableau et regarde l'allure de la courbe obtenue pour voir si les résultats que tu va calculer sont sur la courbe ou en dehors...cohérence oblige !)

f(3/2)=?

pour passer en x de 1 à 2 on a une longueur de 1

donc à 1 (en x) on fait correspondre quoi en y ?

calcul : on fait correspondre la longueur en valeur absolue de Y1-Y2=(1/12)+(4/3)=17/12

donc à 1 correspond 17/12

et à 0.5 correspond x = ? (0.5 est à la moitié entre 1 et 2, donc correspond à 3/2)

REGLE DE TROIS : x=0.5.(17/12)=17/24


17/24 est une valeur de y depuis l'ordonnée de 1

donc ce qu'on cherche c'est donc (1/12) - (17/24) = -15/24

et -15/24=-0.625, d'après moi c'est bien sur ma courbe tracée à main levée, donc ça devrait correspondre....sauf distraction vu le contexte de réveillon de la st sylvestre ! ! ! ...........

donc f(3/2)=-15/24 par interpolation linéaire entre les points d'abscisses 1 et 2

Merci pour ta réponse, j'ai fait une courbe sur le logiciel géogébra et voici ce que ça donne je sais pas trop si c'est bon:

[img][IMG]http://img15.hostingpics.net/pics/4292075a72849d2b301105ba066b0a6ccd0605.gif[/img][/IMG]

[laetidom]

Bonjour Cynthia,

Bonne Année 2015 à tous ! ! !

Les maths quand tu nous tiens !......

D'abord peux-tu me dire à quoi correspond tes 2 équations (droite, f(x) ?)

Ensuite pour moi ce qui relie tous tes points c'est une courbe et je remarque que le y de l'abscisse 1.5 [c'est-à-dire mon f(3/2)] est cohérent par rapport à celui du point d'avant (1) et celui du point d'après (2) donc je devrais être pas trop mal (sous réserve d'une erreur du jour de l'an....-sourire -....)

-------------------------------
peux-tu nous calculer f(3) ?........
-------------------------------

[WillyCagnes]

bjr et bonne Année 2015

tu as vu l'equation
Y=ax+b

avec la pente a=[f(x2)-f(x1)]/(x2-x1)
et b= f(x1)

y=f(x) et on te donne la valeur de x
tu remplaces par les données du tableau

1) x=1,5
f(1,5)= [-16/12 -1/12]/(2-1)[1,5-1] -4/3=-17/12 -1/12=-(17/12)/2-1/12=-15/24

2) tu utilises la même methode pour l'interpolation

f(3)= [(-2/3 +4/3)/(4-2)] (3 -4/3) -4/3 =?

[laetidom]

Merci WillyCagnes (Bonne Année ! ! ! ) pour me permettre de simplifier ma méthode :

f(3/2)=?

interpolation linéaire donc suivant une droite entre points d'abscisses 1 et 2

calcul équation de droite entre 1 et 2 : y=ax+b

si M sur droite (12) alors:
1M = k.12
xM-x1=k.(x2-x1) idem pour y :

x-1=k
y-(1/12)=(-17/12).k

d'où (k=)x-1=(y-(1/12))/(-17/12)

d'où droite (12) d'équation y=-x+

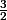
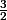
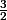
en 1) on nous demande pour x=1.5 [compris entre 1 et 2] donc y =-.+=- comme trouvé hier soir mais moins alambiqué !...............

Bonne 1ère journée ensoleillée de 2015 ! ! !

[laetidom]

pour la 1) et la 2) on donne x et on cherche y

pour la 3) on donne y (f(x)=0 imposé) et on cherche x

[laetidom]

même topo : équation de la droite (45) puisqu'on nous dit que "la solution de f(x)=0 est supérieure à 4..." ce que je constate sur mon tracé à main levée :

===> droite (45) d'équation y= x -25

On nous dit que f(x)=0 donc que y=0, ce qui donne :

y= x -25=0 ====> x=25.

x==env à 4.109......ce qui est bien supérieur à 4 comme stipulé dans l'énoncé !.....

Bonne journée

[Cynthia37200]

bjr et bonne Année 2015

tu as vu l'equation
Y=ax+b

avec la pente a=[f(x2)-f(x1)]/(x2-x1)
et b= f(x1)

y=f(x) et on te donne la valeur de x
tu remplaces par les données du tableau

1) x=1,5
f(1,5)= [-16/12 -1/12]/(2-1)[1,5-1] -4/3=-17/12 -1/12=-(17/12)/2-1/12=-15/24

2) tu utilises la même methode pour l'interpolation

f(3)= [(-2/3 +4/3)/(4-2)] (3 -4/3) -4/3 =?

Bonjour bonne année 2015,

J'ai trouvé -2,7 mais j'ai l'impression que le résultat n'est pas plausible.

[Cynthia37200]

Bonjour Cynthia,

Bonne Année 2015 à tous ! ! !

Les maths quand tu nous tiens !......

D'abord peux-tu me dire à quoi correspond tes 2 équations (droite, f(x) ?)

Ensuite pour moi ce qui relie tous tes points c'est une courbe et je remarque que le y de l'abscisse 1.5 [c'est-à-dire mon f(3/2)] est cohérent par rapport à celui du point d'avant (1) et celui du point d'après (2) donc je devrais être pas trop mal (sous réserve d'une erreur du jour de l'an....-sourire -....)

-------------------------------
peux-tu nous calculer f(3) ?........
-------------------------------

f(3) = = 2/3/2 x 5/3 x -4/3 = 1/3 x 5/3 x -4/3 = -20/27

[Cynthia37200]

même topo : équation de la droite (45) puisqu'on nous dit que "la solution de f(x)=0 est supérieure à 4..." ce que je constate sur mon tracé à main levée :

===> droite (45) d'équation y= x -25

On nous dit que f(x)=0 donc que y=0, ce qui donne :

y= x -25=0 ====> x=25.

x==env à 4.109......ce qui est bien supérieur à 4 comme stipulé dans l'énoncé !.....

Bonne journée

f(3)= -2/3+4/3=2/3
[(-2/3 +4/3)/(4-2)] (3 -4/3) -4/3 =(2/3/2)((9-4)/3)-4/3
=(4/3x5/3)-4/3
=20/9-4/3
=(20-12)/9
=8/9

[Cynthia37200]

bjr et bonne Année 2015

tu as vu l'equation
Y=ax+b

avec la pente a=[f(x2)-f(x1)]/(x2-x1)
et b= f(x1)

y=f(x) et on te donne la valeur de x
tu remplaces par les données du tableau

1) x=1,5
f(1,5)= [-16/12 -1/12]/(2-1)[1,5-1] -4/3=-17/12 -1/12=-(17/12)/2-1/12=-15/24

2) tu utilises la même methode pour l'interpolation

f(3)= [(-2/3 +4/3)/(4-2)] (3 -4/3) -4/3 =?

f(3)= f(3)= -2/3+4/3=2/3
[(-2/3 +4/3)/(4-2)] (3 -4/3) -4/3 =(2/3/2)((9-4)/3)-4/3
=(4/3x5/3)-4/3
=20/9-4/3
=(20-12)/9
=8/9

[laetidom]

f(3)= f(3)= -2/3+4/3=2/3
[(-2/3 +4/3)/(4-2)] (3 -4/3) -4/3 =(2/3/2)((9-4)/3)-4/3
=(4/3x5/3)-4/3
=20/9-4/3
=(20-12)/9
=8/9

Rebonjour,

je vérifie avec ma méthode je trouve f(3)=-1 ce que je trouve cohérent me semble-t-'il par rapport aux y de 2 et 4 .....par la méthode de WillyCagnes je trouve -7/9 ce qui est proche de la mienne, signe ok et cohérent, écart de valeur ?, par contre ton résultat de +8/9 !? ça ne peut pas être positif ! regarde la courbe....je cherche....

[Cynthia37200]

Rebonjour,

je vérifie avec ma méthode je trouve f(3)=-1 ce que je trouve cohérent me semble-t-'il par rapport aux y de 2 et 4 .....par la méthode de WillyCagnes je trouve -7/9 ce qui est proche de la mienne, signe ok et cohérent, écart de valeur ?, par contre ton résultat de +8/9 !? ça ne peut pas être positif ! regarde la courbe....je cherche....

J'ai refait le calcul et je trouve un nombre négatif:
= 2/3/2 x 5/3 x -4/3
= 1/3 x 5/3 x -4/3 = -20/27

[laetidom]

J'ai refait le calcul et je trouve un nombre négatif:
= 2/3/2 x 5/3 x -4/3
= 1/3 x 5/3 x -4/3 = -20/27

Ah déjà un nombre négatif c'est mieux !!!

Si quelqu'un pouvait nous départager pour être sûr de la bonne valeur ! ça serait super, merci

[Cynthia37200]

Ah déjà un nombre négatif c'est mieux !!!

Si quelqu'un pouvait nous départager pour être sûr de la bonne valeur ! ça serait super, merci

Il y a peut-être plusieurs réponses non ? Si on remonte un peu plus en haut en utilisant différentes méthodes tu as trouvé deux résultats.

[laetidom]

Il y a peut-être plusieurs réponses non ? Si on remonte un peu plus en haut en utilisant différentes méthodes tu as trouvé deux résultats.

Ah non Cynthia, ici il n'y a pas deux résultats possibles !,relis bien mes messages, j'ai trouvé deux fois le même résultat en ayant modifié ma méthode, le résultat qui différait résultait de la méthode de Willy....

[danyL]

il y a une petite erreur dans le remplacement de x par 3 :
f(3)= [(-2/3 +4/3)/(4-2)] (3 -4/3) -4/3 =?

"x" a été remplacé par "(3 -4/3)" au lieu de simplement "3"

[laetidom]

il y a une petite erreur dans le remplacement de x par 3 :
f(3)= [(-2/3 +4/3)/(4-2)] (3 -4/3) -4/3 =?

"x" a été remplacé par "(3 -4/3)" au lieu de simplement "3"

Bonjour danyL,

merci pour avoir répondu au post de Cynthia, si je calcule ton f(3) ça ferait =-2/3, c'est ça ?

je ne comprends pas pourquoi moi je trouve -1 ? (déjà le -4/3 si j'ai bien compris la méthode de Willy c'est b=f(x1) mais déjà je ne vois pas pourquoi b serait égal à f(x1) ? --- Ah si je pense que l'ordonnée de son repère passe par x1, c'est ça ????? -------oui mais maintenant si je calcule par sa méthode je retrouve bien mon -1, je n'y comprends RIEN !!!!! HELP !!!!!! ---peux-tu me renseigner à ce sujet ?......histoire que l'on puisse donner à Cynthia une réponse ferme et définitive, je t'en remercie par avance !)

[danyL]

oui tu as raison Laetidom ce n'est pas encore bon
il faudrait demander plutot à Willy pourquoi il dit que b = f(x1)

pour Cynthia :
interpolation linéaire : on connait seulement certains points appartenant à une courbe, et on cherche à calculer (estimer) les points intermédiaires
pour cela, on va supposer qu'entre 2 points connus M1 et M2 la courbe est tout simplement une droite (d'où l'adjectif "linéaire", il existe d'autres formes d'interpolation plus complexes)
pour calculer l'ordonnée d'un point M entre ces 2 points (x1 < xM < x2), on considère donc que M est sur le segment de droite qui passe par M1 et M2

on cherche d'abord l'équation de la droite y=a * x + b qui passe par les 2 points M1(x1=2, f(x1)=-4/3) et M2(x2=4, f(x2)=-2/3)
comme M1 et M2 font partie de la droite que l'on cherche, ils satisfont aux équations :
f(x1) = a * x1 + b
f(x2) = a * x2 + b

la pente (coefficient directeur) est bien a=[f(x2)-f(x1)]/(x2-x1)
soit ici a = [-2/3 - (-4/3)]/(4-2) = [2/3]/2 = 1/3

on calcule b avec par exemple le premier point M1 : (mais il existe peut etre une méthode plus simple)
f(x1) = a * x1 + b
soit ici :
-4/3 = (1/3) * 2 + b
d'où b = (-4/3) * (3/2) = -2

la droite qui passe par M1 et M2 a donc pour équation :
y = 1/3 * x -2

pour estimer l'ordonnée de x3=3 par interpolation linéaire, on dit que le point M3(x3, f(x3)) est sur cette droite :
f(x3) = 1/3 * 3 - 2
f(x3) = -1