Petite question
4 messages
- Page 1 sur 1
Petite question
Bonjour, soit  un
un  -espace vectoriel (je ne sais pas s'il faut qu'il soit fini ou non...) ; on se donne un endomorphisme d'espaces vectoriels
-espace vectoriel (je ne sais pas s'il faut qu'il soit fini ou non...) ; on se donne un endomorphisme d'espaces vectoriels  . Le problème est que je ne comprends pas pourquoi
. Le problème est que je ne comprends pas pourquoi = {\rm id}_E) ,
,  désigne le polynôme constant égal à
désigne le polynôme constant égal à  dans
dans 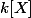 . Merci d'avance :we:
. Merci d'avance :we:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Bonjour, soitun
-espace vectoriel (je ne sais pas s'il faut qu'il soit fini ou non...) ; on se donne un endomorphisme d'espaces vectoriels
. Le problème est que je ne comprends pas pourquoi
,
désigne le polynôme constant égal à
dans
. Merci d'avance :we:
Dans L(E), les polynômes en f forment une sous structure (sous algèbre de L(E) sur K pour +, o).
L'image de la base canonique de K[X] (1,X,X^2,...) par le morphisme X->f est bien (Id, f, fof, ... ).
On peut donc voir Id comme le polynôme constant 1 appliqué à f.
En fait on dispose d'une application de "représentation" K[X] dans L(E) qui à un polynôme P associe l'application linéaire P(f).
Luc
Luc a écrit:Dans L(E), les polynômes en f forment une sous structure (sous algèbre de L(E) sur K pour +, o).
L'image de la base canonique de K[X] (1,X,X^2,...) par le morphisme X->f est bien (Id, f, fof, ... ).
On peut donc voir Id comme le polynôme constant 1 appliqué à f.
En fait on dispose d'une application de "représentation" K[X] dans L(E) qui à un polynôme P associe l'application linéaire P(f).
Luc
Ok, merci.
Je croyais qu'il y avait trois lois de compositions dans une algèbre
Oui, le morphisme d'évaluation il me semble :
Merci :+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
