Système linéaire à paramètres

par **Mayhem** » 29 Déc 2014, 14:09

Bonjour, j'ai quelques difficultés pour résoudre ce système qui a pour paramètres m et a.

J'ai commencé à le résoudre ce qui donne :

L2<-- L2-aL1
L3<-- L3-L1

Ce qui donne

A partir d'ici je suis bloqué, si vous pouviez m'aider. :/

Merci d'avance.

par **Sake** » 29 Déc 2014, 14:31

Dans quelles conditions la matrice

a-t-elle un inverse ? Dans ces cas, le calculer.

par **Mayhem** » 29 Déc 2014, 14:42

Euh, m'expliquer le rapport avec les matrices ?
Surtout que je n'ai pas encore abordé ce chapitre..

par **Sake** » 29 Déc 2014, 14:57

Mayhem a écrit:Euh, m'expliquer le rapport avec les matrices ?
Surtout que je n'ai pas encore abordé ce chapitre..

Ton système s'écrit indifféremment :

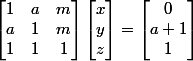
ce qui se note encore

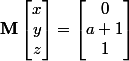
Ici, il faut pouvoir inverser M pour trouver

par **Mayhem** » 29 Déc 2014, 15:10

Je n'ai pas encore abordé les matrices, je ne dois pas résoudre le système ainsi..

par **Sake** » 29 Déc 2014, 15:26

Mayhem a écrit:Bonjour, j'ai quelques difficultés pour résoudre ce système qui a pour paramètres m et a.

J'ai commencé à le résoudre ce qui donne :

L2<-- L2-aL1
L3<-- L3-L1

Ce qui donne

A partir d'ici je suis bloqué, si vous pouviez m'aider. :/

Merci d'avance.

Tu peux additionner les deux dernières lignes pour trouver z, et ensuite trouver y.

Système linéaire à paramètres

Système linéaire à paramètres

Qui est en ligne